K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
28 tháng 12 2019
Chọn B.
Ta có :
2 - x = 0 ⇔ x = 2
2x + 1 = 0 ⇔ x = -1/2
Xét dấu f(x):
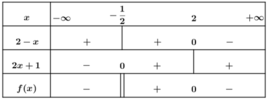
Vậy f(x) ≥ 0 khi
PT
1
CM
26 tháng 3 2017
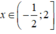
Đáp án: B
Điều kiện xác định của phương trình là 
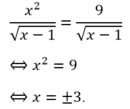
Kết hợp với điều kiện của phương trình ta được 
là nghiệm của phương trình.
⇒ Phương trình có 1 nghiệm.
PT
1
CM
31 tháng 8 2017
Chọn A.
Điều kiện: x > 1
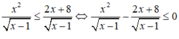
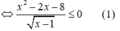
Vì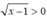 
với ∀x > 1 nên bất phương trình (1) tương đường với x2 - 2x - 8 ≤ 0 ⇔ -2 ≤ x ≤ 4.
Kết hợp với điều kiện x > 1 suy ra 1 ≤ x ≤ 4 ⇒ x ∈ {2;3;4}
Vậy bất phương trình có ba nghiệm nguyên.
NT
1
9 tháng 6 2022
a: \(-x^2+4x+1\)
\(=-\left(x^2-4x-1\right)\)
\(=-\left(x^2-4x+4-5\right)\)
\(=-\left(x-2\right)^2+5\le5\)
Dấu '=' xảy ra khi x=2
b: \(x^2+2x+6=\left(x+1\right)^2+5\)
\(\Leftrightarrow\dfrac{2000}{\left(x+1\right)^2+5}\le400\)
Dấu '=' xảy ra khi x=-1
c: \(-9x^2+6x+19\)
\(=-\left(9x^2-6x-19\right)\)
\(=-\left(9x^2-6x+1-20\right)\)
\(=-\left(3x-1\right)^2+20\le20\)
Dấu '=' xảy ra khi x=1/3
d: \(=-\left(x^2+4x+y^2-2y\right)\)
\(=-\left(x^2+4x+4+y^2-2y+1-5\right)\)
\(=-\left(x+2\right)^2-\left(y-1\right)^2+5\le5\)
Dấu '=' xảy ra khi x=-2 và y=1
CM
23 tháng 10 2019
Điều kiện xác định: x – 2 > 0 ⇔ x > 2.
Khi đó (3) ⇔ x2 = 8 ⇔ x = –2√2 (không t/m đkxđ)
hoặc x = 2√2 (t/m đkxđ)
Vậy phương trình có nghiệm là: x = 2√2.
5 tháng 11 2017
\(\left(x+2\right)\left(3-4x\right)=x^2+4x+4\\ \Leftrightarrow6-5x-4x^2=x^2+4x+4\\ \Leftrightarrow5x^2+9x-2=0\\ \Leftrightarrow5\left(x+\dfrac{9}{10}\right)^2=\dfrac{121}{20}\\ \Leftrightarrow\left(x+\dfrac{9}{10}\right)^2=\dfrac{\dfrac{121}{20}}{5}=\dfrac{121}{100}\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{9}{10}=\dfrac{11}{10}\\x+\dfrac{9}{10}=-\dfrac{11}{10}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=2\end{matrix}\right.\)
vậy x cần tìm là 0,2 và 2
TT
1
a)\(2^x=16\)
\(\Leftrightarrow2^x=2^4\)
\(\Leftrightarrow x=4\)
b)\(3^{x+1}=9^x\)
\(\Leftrightarrow3^{x+1}=\left(3^2\right)^x\)
\(\Leftrightarrow3^{x+1}=3^{2x}\)
\(\Leftrightarrow x+1=2x\)
\(\Leftrightarrow x=1\)
c)\(2^{3x+2}=4^{x+5}\)
\(\Leftrightarrow2^{3x+2}=\left(2^2\right)^{x+5}\)
\(\Leftrightarrow2^{3x+2}=2^{2\left(x+5\right)}\)
\(\Leftrightarrow3x+2=2\left(x+5\right)\)
\(\Leftrightarrow3x+2=2x+10\)
\(\Leftrightarrow x=8\)
d)\(3^{2x+1}=243\)
\(\Leftrightarrow3^{2x+1}=3^5\)
\(\Leftrightarrow2x+1=5\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
\(2^{\text{ }x}=16\)
\(2^x=2^4\)
\(\Rightarrow x=4\)
Vậy \(x=4\)