K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Bài 1.
25 tháng 10 2020
Đề:............
<=> - (1 - 2018x) + 2019x.(1 - 2018x) = 0
<=> (1 - 2018x).[(-1) + 2019x] = 0
Xét 2 trường hợp, ta có:
TH1: 1 - 2018x = 0 TH2: -1 + 2019x = 0
<=> 2018x = 1 <=> 2019x = 1
<=> x = 1/2018 <=> x = 1/2019
Vậy x = 1/2018; 1/2019
9 tháng 11 2018
\(2018x-1+2019x\left(1-2018x\right)=0\)
\(-\left(1-2018x\right)+2019x\left(1-2018x\right)=0\)
\(\left(1-2018x\right)\left(-1+2019x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}1-2018x=0\\-1+2019x=0\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2018}\\x=\frac{1}{2019}\end{cases}}}\)
LT
2
18 tháng 1 2020
a) 3x(x - 1) + 7x2(x - 1) = 0
<=> x(x - 1)(3 + 7x) = 0
<=> x = 0
hoặc : x - 1 = 0
hoặc 3 + 7x = 0
<=> x = 0
hoặc x = 1
hoặc x = -3/7
b) x2 - 2018x - 2019 = 0
<=> x2 - 2019x + x - 2019 = 0
<=> x(x - 2019) + (x - 2019) = 0
<=> (x + 1)(x - 2019) = 0
<=> \(\orbr{\begin{cases}x+1=0\\x-2019=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-1\\x=2019\end{cases}}\)
c) (x + 3)2 - x(x - 2) = 13
<=> x2 + 6x + 9 - x2 + 2x = 13
<=> 8x = 13 - 9
<=> 8x = 6
<=> x= 6/8 = 3/4
A
18 tháng 1 2020
a/\(3x\left(x-1\right)+7x^2\left(x-1\right)=0.\)
\(\Leftrightarrow\left(x-1\right)\left(3x+7x^2\right)=0\)
\(\Leftrightarrow\left(x-1\right)x\left(3+7x\right)=0\)
Th1: x - 1 = 0
=> x = 1
Th2: x= 0
Th3: 3 + 7x = 0
=> x= -3/7
\(\Rightarrow x\in\left\{1;0;-\frac{3}{7}\right\}\)
b/ \(x^2-2018x-2019=0\)
\(\Leftrightarrow x^2+x-2019x-2019=0\)
\(\Leftrightarrow\left(x^2+x\right)-\left(2019x+2019\right)=0\)
\(\Leftrightarrow x\left(x+1\right)-2019\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-2019\right)\left(x+1\right)=0\)
Th1 : x -2019 = 0
=> x =2019
Th2: x + 1 =0
=> x = -1
\(\Rightarrow x\in\left\{2019;-1\right\}\)
c/ \(\left(x+3\right)^2-x\left(x-2\right)=13\)
\(\Leftrightarrow x^2+6x+9-x^2+2x=13\)
\(\Leftrightarrow8x=4\Rightarrow x=\frac{1}{2}\)
8 tháng 11 2018
\(2018x^2-2019x+1=0\)
\(2018x^2-2018x-x+1=0\)
\(2018x\left(x-1\right)-\left(x-1\right)=0\)
\(\left(x-1\right)\left(2018x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\2018x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\x=\frac{1}{2018}\end{cases}}}\)
HH
2
HN
20 tháng 2 2019
a) \(x^4+2019x^2+2018x+2019\)
\(=\left(x^4-x\right)+\left(2019x^2+2019x+2019\right)\)
\(=x\left(x^3-1\right)+2019\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x^2+x+1\right)+2019\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left[x\left(x-1\right)+2019\right]\)
\(=\left(x^2+x+1\right)\left(x^2-x+2019\right)\)
b) \(E=2x^2-8x+1=2x^2-8x+8-7\)
\(=2\left(x^2-4x+4\right)-7=2\left(x-2\right)^2-7\)
Vì \(2\left(x-2\right)^2\ge0\forall x\Rightarrow E\ge-7\)
Dấu "=" xảy ra <=> \(2\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)
Vậy MinE = -7 <=> x = 2
20 tháng 2 2019
b) \(E=2x^2-8x+1\)
\(E=2\left(x^2-4x+\frac{1}{2}\right)\)
\(E=2\left(x^2-2\cdot x\cdot2+2^2+\frac{7}{2}\right)\)
\(E=2\left[\left(x-2\right)^2+\frac{7}{2}\right]\)
\(E=2\left(x-2\right)^2+7\ge7\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x-2=0\Leftrightarrow x=2\)
Vậy....
KB
0
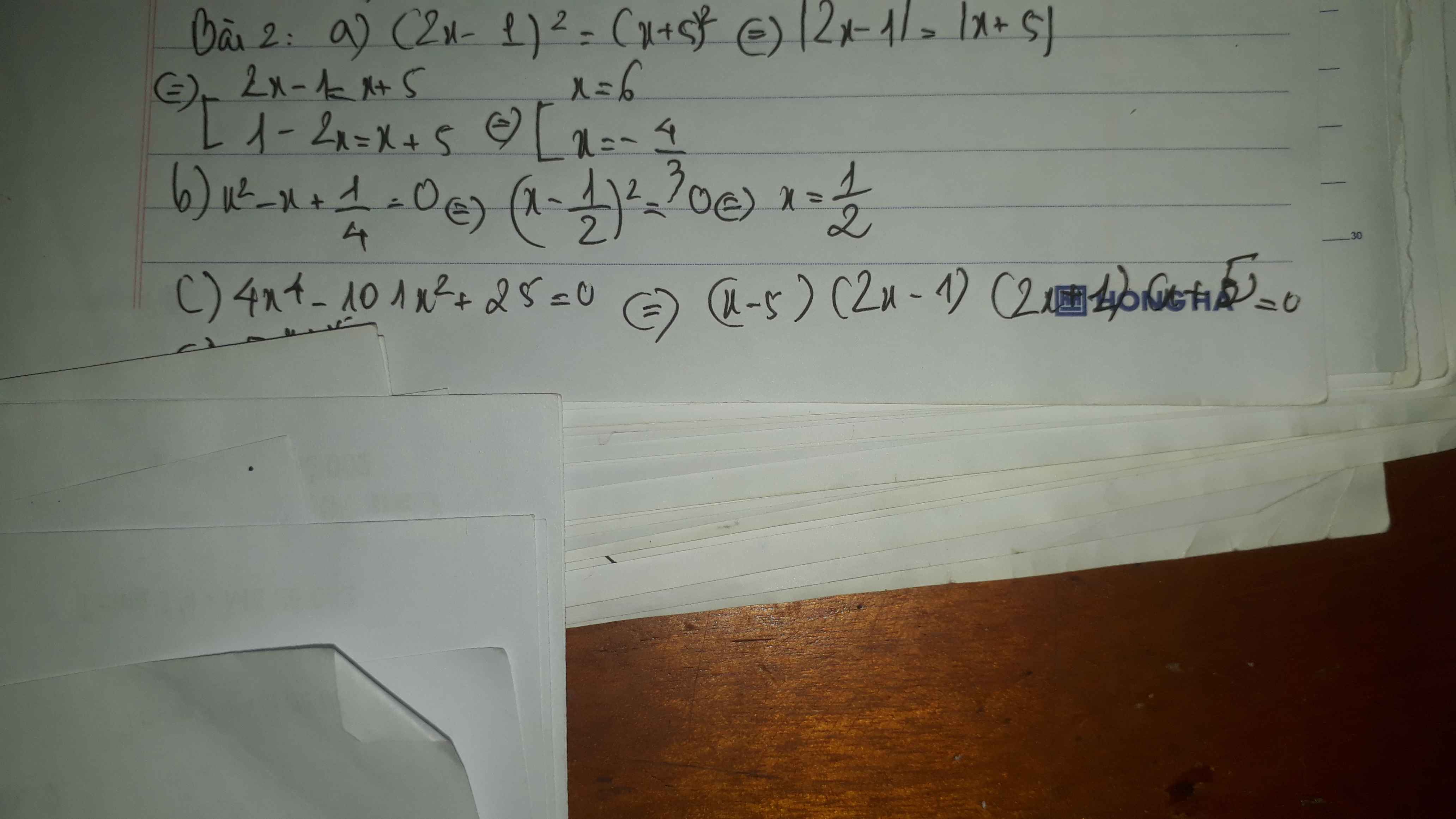
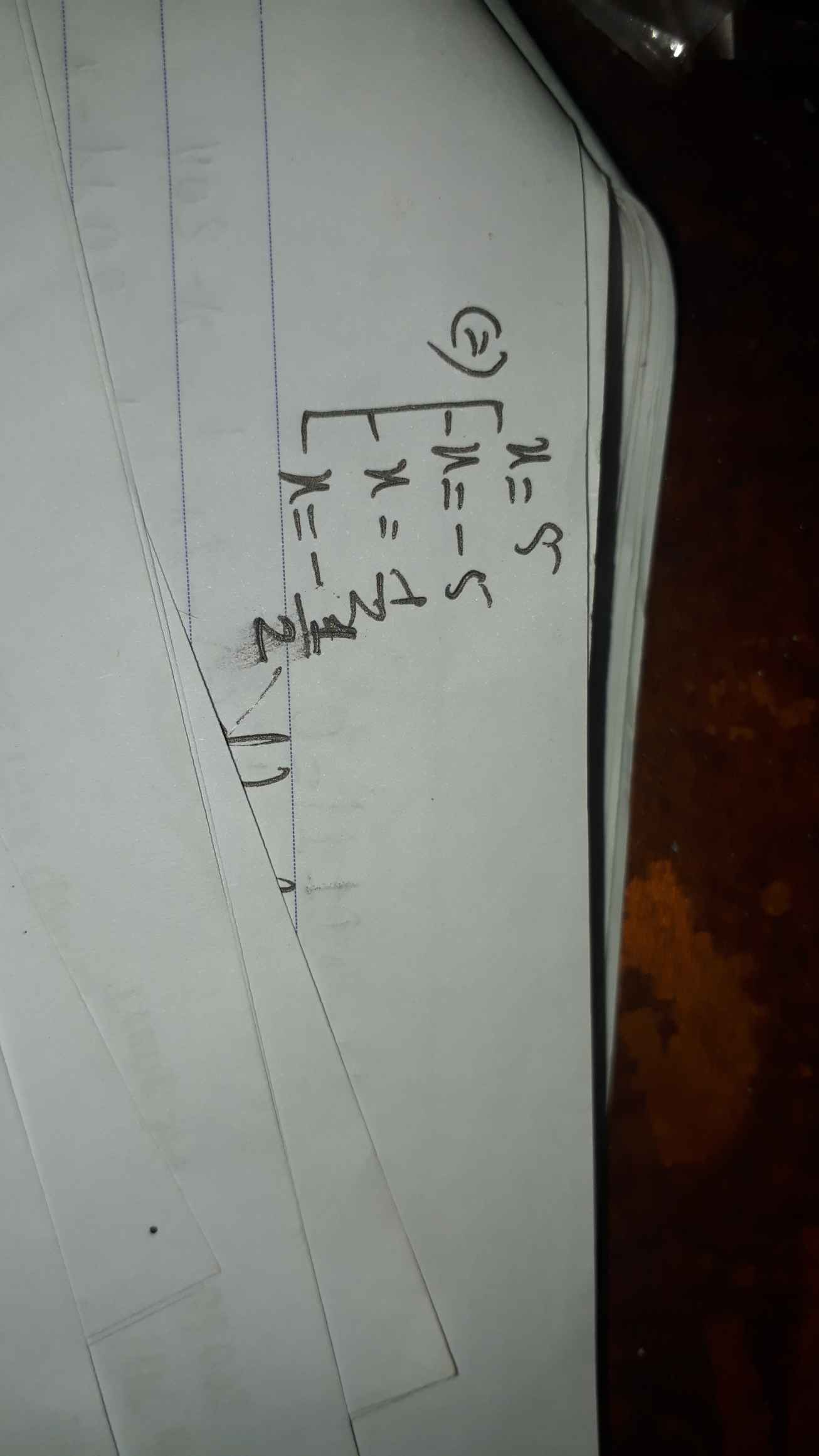
pt \(\Leftrightarrow x^2+x-2019x-2019=0\)
\(\Leftrightarrow x\left(x+1\right)-2019\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2019\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2019\end{matrix}\right.\)
Vậy ...
huhu bạn ơi hình như sai đề rồi á