Xét khai triển (1+x)(1+2x)(1+3x)....(1+2019x) = a0 + a1x + a2x2 + a3x3 +...+ a2019x2019. Tính S = 2a2 + (11 + 22 +...+ 20192)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 8 2017
Chọn đáp án D
Ta có
nên a k = C n k ( - 2 ) k
⇒ a k = 2 k . C n k với 0 ≤ k ≤ n , k ∈ ℕ Suy ra
Xét khai triển
Đạo hàm hai vế của (*):
Nhân cả hai vế của (**) với x:
Thay x=2 vào (1) ta được
⇔ n . 3 n = 52488 = 8 . 3 8 . Suy ra n = 8
Vậy với n = 8 thì P = 390625
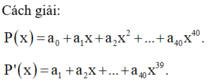
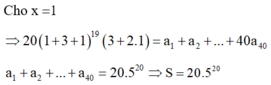
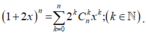
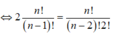
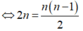
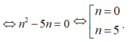
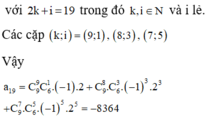
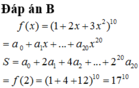
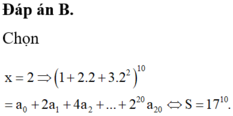
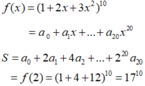
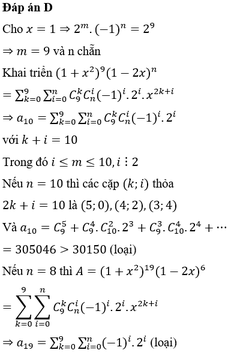
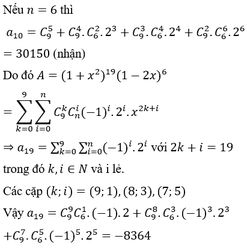
\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)-1\)
\(=x+\sum\limits^n_{k=2}kx\left(1+x\right)...\left(1+\left(k-1\right)x\right)\)
\(=x+\sum\limits^n_{k=2}kx\left[\left(1+x\right)...\left(1+\left(k-1\right)x\right)-1+1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left[\left(1+x\right)\left(1+2x\right)...\left(1+\left(k-1\right)x\right)-1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left(\sum\limits^{k-1}_{i=1}ix\left(1+x\right)\left(1+2x\right)...\left(1-\left(i-1\right)x\right)\right)\)
Do đó tổng của các hệ số chứa \(x^2\) là: \(\sum\limits^n_{k=2}k\left(\sum\limits^{k-1}_{i=1}i\right)\)
Hay \(a_2=\sum\limits^n_{k=2}k\left(\frac{k\left(k-1\right)}{2}\right)=\sum\limits^n_{k=2}\frac{k^2\left(k-1\right)}{2}\)
Do đó:
\(S=1+\sum\limits^{2019}_{k=2}\frac{k^2\left(k-1\right)}{2}+\sum\limits^{2019}_{k=2}k^2=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k-1\right)}{2}+k^2\right)\)
\(=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k+1\right)}{2}\right)\)
thanks,đã giúp r mong bạn giúp luôn câu hình học mk vs