Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
+) Khẳng định i): a > 2019 thì a x > 2019 x ∀ x ∈ ℝ ⇒ x = 1 khẳng định sai.
+) Khẳng định ii): a > 2019 thì b a > b 2019 ∀ b > 0 ⇔ b > 0 khẳng định sai.
+) Khẳng định iii): a > 2019 thì log b a > log b 2019 ∀ n > 0 ; b ≢ 0 ⇔ b > 1 khẳng định sai
Chọn A.

Ta có
lim x → 1 f x - f 1 x - 1 = lim x → 1 x - 1 x - 2 x - 3 . . . x - 2019 x - 1 = lim x → 1 x - 1 x - 2 x - 3 . . . x - 2019 = - 1 . - 2 . - 3 . . . . - 2018 = 2018 !
Đáp án C

a: =>x+3>0
hay x>-3
b: \(\Leftrightarrow-\left(x-2\right)^2\left(x+2\right)>0\)
=>x+2<0
hay x<-2
c: =>x+4>0
hay x>-4
d: =>-3<x<4

y’= -2f’(x) nên hàm số nghịch biến trên (-∞;-2),(-1;2) và (4;+∞).
Chọn đáp án B.

Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 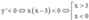 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞





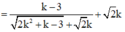

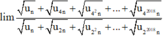
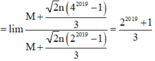 .
.