Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)
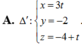

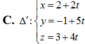
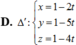


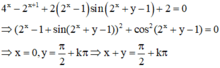

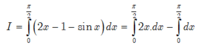
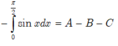
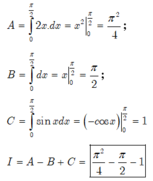
Đáp án B