Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TẤT CẢ BÀI TRÊN ĐỀU LÀ CHƯƠNG TRÌNH VNEN CÁC BẠN LÀM ĐẦY ĐỦ VÀ CHÍNH XÁC NHÉ
MÌNH ĐANG CẦN GẤP , NGÀY MAI CÔ KIỂM TRA RÙI
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1.
a)

b)

Thực hiện đo các góc của \(\Delta EFG\), ta có:
\(\widehat{E}=\widehat{F}=\widehat{G}=60^0.\)
c) Các bước chứng minh bài toán lần lượt là: iv → ii → I → iii.
2.
b)
Chúc bạn học tốt!

a: Xét ΔOMA và ΔOMB có
OM chung
MA=MB
OA=OB
Do đó: ΔOMA=ΔOMB
Xét ΔONA và ΔONB có
ON chung
NA=NB
OA=OB
Do đó: ΔONA=ΔONB
b: Ta có: OA=OB
nen O nằm tren đường trung trực của AB(1)
Ta có: MA=MB
nen M nằm trên đường trung trực của AB(2)
Ta có: NA=NB
nên N nằm trên đường trung trực của AB(3)
TỪ (1), (2)và (3) suy ra O,M,N thẳng hàng
c: Xét ΔAMN và ΔBMN có
AM=BM
MN chung
AN=BN
Do đó ΔAMN=ΔBMN

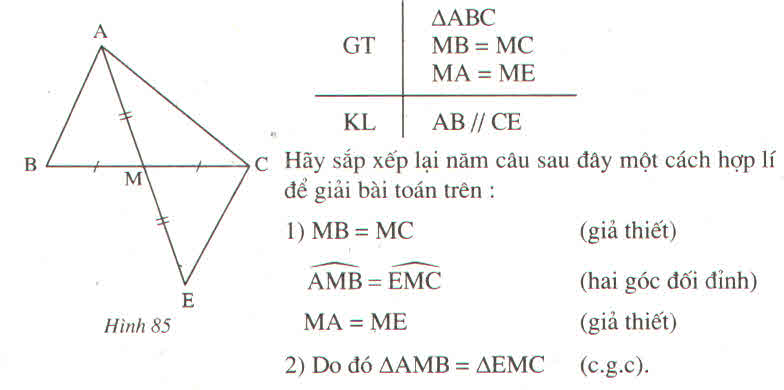
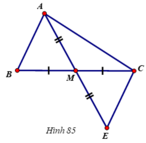
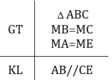
- Thứ tự sắp xếp là 5, 1, 2, 4, 3
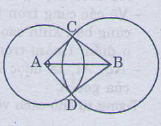
Tam giác AMB và tam giác EMC có
MB = MC (gt)
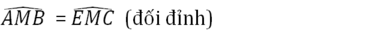
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


a) Xét \(\Delta\)OMA và \(\Delta\)OMB:
OA = OB (đề bài)
AM = BM (vì có cùng bán kính)
Cạnh OM chung
=> \(\Delta\)OMA = \(\Delta\)OMB (c.c.c)
Xét \(\Delta\)ONA và \(\Delta\)ONB
OA = OB (đề bài)
AN = BN (vì cò cùng bán kính)
Cạnh ON chung
=> \(\Delta\)ONA = \(\Delta\)ONB (c.c.c)
b) Ta có \(\Delta\)OMA = \(\Delta\)OMB (theo câu a)
=> ^AOM = ^BOM (2 góc tương ứng)
=> OM là tia phân giác của ^AOB
Lại có \(\Delta\)ONA = \(\Delta\)ONB (theo câu a)
=> ^AOM = ^BOM (2 góc tương ứng)
=> ON là tia phân giác của ^AOB
Mà mỗi góc chỉ có duy nhất một tia phân giác
=> OM và ON trùng nhau
hay O, M, N thẳng hàng (ĐPCM)
c) Xét \(\Delta\)AMN và \(\Delta\)BMN
AM = BM (vì có cùng bán kính)
AN = BN (vì có cùng bán kính)
cạnh MN chung
=> \(\Delta\)AMN = \(\Delta\)BMN (c.c.c)
d) Ta có \(\Delta\)AMN = \(\Delta\)BMN (theo câu c)
=> ^AMN = ^BMN (2 góc tương ứng)
=> MN là tia phân giác của ^AMB
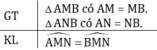
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có
Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
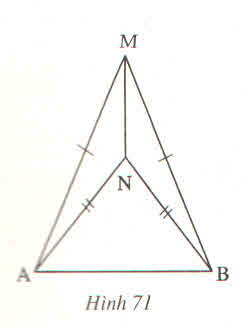
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg