Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
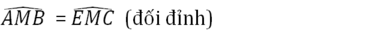
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg

b: \(\widehat{C}=60^0\)
c: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
d: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AB//CD
e: Ta có: ΔCBA vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2
hay BC=2AM

GT : \(\Delta ABC\); AB = AC ; BM = MC ( M \(\in\)BC ) ; \(\widehat{B}=40^o\)
KL : b) \(\Delta AMB=\Delta AMC\)
c) \(\widehat{BAM}=?\)
giải
b) vì \(\Delta ABC\)cân tại A nên AB = AC
M là trung điểm của BC nên BM = MC = \(\frac{BC}{2}\)
Xét \(\Delta AMB\)và \(\Delta AMC\)có :
AB = AC ( gt )
BM = MC ( gt )
AM ( cạnh chung )
Suy ra : \(\Delta AMB\)= \(\Delta AMC\)( c.c.c )
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)( 2 góc tương ứng )
c) vì \(\Delta ABC\)cân tại A nên \(\widehat{B}=\widehat{C}=40^o\)
\(\Rightarrow\widehat{BAC}=180^o-\left(40^o+40^o\right)=100^o\)
Mà \(\widehat{BAC}=\widehat{BAM}+\widehat{CAM}\)
\(\Rightarrow\widehat{BAM}=\frac{100^o}{2}=50^o\)
vì tg ABC cân ở a=> góc B= gócC=40độ
b) * Xét tg AMB và tg AMC
+)AB=AC(Vì tg ABC cân ở A)
+) gócB= gócC (cmt)
+)BM=MC (vì M là trg điểm của BC)
=>tgAMB=tgAMC (CGC)
c)*Xét tg ABC :BAC+B+C=180độ
<=>BAC+40độ+40độ=180độ
=>BAC=100độ (1)
lại có tgAMB=tgAMC (cmt)
=>góc BAM=gócMAC (2)
Từ(1),(2)=>Góc BAM=góc MAC=100:2=50độ
=>góc BAM=50 độ (đpcm)

b: Xét ΔOMA vuông tại A và ΔOMB vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
DO đó: ΔOMA=ΔOMB
Suy ra: OA=OB
hay ΔOAB cân tại O
c: Xét ΔOEF có
ON là đường cao
ON là đường phân giác
Do đó: ΔOEF cân tại O
Suy ra: OE=OF
Xét ΔOBA có
OE/OA=OF/OB
Do đó: EF//AB
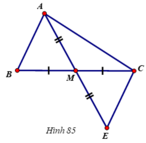
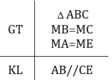
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có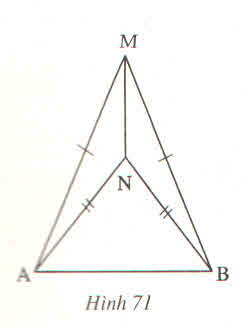

Ghi giả thiết và kết luận: