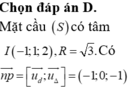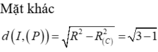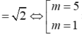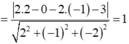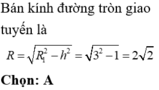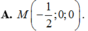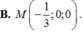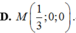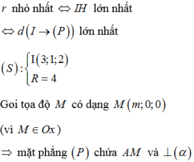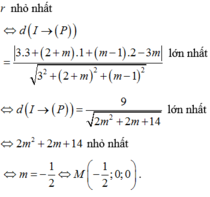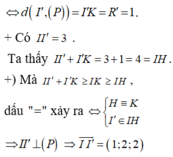Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Gọi I (m; 0; 0) là tâm mặt cầu có bán kính R, d1, d2 là các khoảng cách từ I đến (P) và (Q).
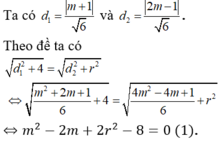
Yêu cầu bài toán tương đương phương trình (1) có đúng một nghiệm m
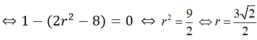
Chọn C
* Ta có: 
trong đó a;b;c không đồng thời bằng 0. Mặt cầu (S) có tâm I (1;2;3) và bán kính R=5.
Do mặt phẳng (P) chứa đường thẳng AB nên ta có:
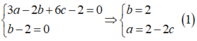
* Bán kính đường tròn giao tuyến là 
trong đó
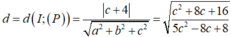
Để bán kính đường tròn nhỏ nhất điều kiện là d lớn nhất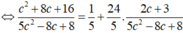 
lớn nhất 
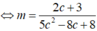lớn nhất.
Coi hàm số 
là một phương trình ẩn c ta được
5mc²-2 (4m+1)c+ (8m-3)=0,
phương trình có nghiệm c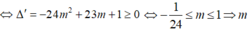 
lớn nhất
<=> c = 1 => a = 0 => M = 2a + b – c = 1
Đáp án A
Vì mặt phẳng (P) đi qua A, B nên
3 a - 2 b + 6 c - 2 = 0 b = 2 ⇔ a = 2 - 2 c b = 2 ⇒ ( P ) : ( 2 - 2 c ) x + 2 y + c z = 0
Khoảng cách từ tâm I (1;2;3) của (S) đến (P) là:
d(I,(P))= ( 2 - 2 c ) + 2 . 2 + c . 3 - 2 ( 2 - 2 c ) 2 + 2 2 + c 2 = c + 4 5 c 2 - 8 c + 8
Khi đó bán kính của đường tròn giao tuyến là:
r= 25 - ( c + 4 ) 2 5 c 2 - 8 c + 8 = 124 c 2 - 208 c + 184 5 c 2 - 8 c + 8
Để r đạt giá trị nhỏ nhất thì hàm số
f(t)= 124 t 2 - 208 t + 184 5 t 2 - 8 t + 8 trên [1;+ ∞ ) phải nhỏ nhất
Ta có: f'(t)= 48 t 2 + 144 t - 192 ( 5 t 2 - 8 t + 8 ) 2 ,
f'(t)=0
⇔
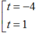
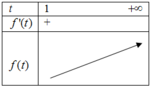
Khi đó hàm số đạt giá trị nhỏ nhất tại t=1 ⇒ c=1
Ta có: T=a+b+c=2-2c+2=4-c=3
