
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài này có 1 số trường hợp hình, tương ứng với mỗi trường hợp sẽ là 1 cách giải, các cách giải khá giống nhau. Ở đây t lm trường hợp đơn giản nhất: A'B' và C'D' có điểm trong chung tức là C' nằm giữa A' và B'; B' nằm giữa C' và D'
Từ A hạ đường vuông góc với BB' tại H
Từ C hạ đường vuông góc với DD' tại K
Gọi I là giao điểm của CD và BB'
Dễ thấy BB' // DD' do cùng _|_ A'D'
=> BID = IDK (so le trong)
Lại có: ABI = BID (so le trong)
=> IDK = ABI
Xét t/g ABH vuông tại H và t/g CDK vuông tại K có:
AB = CD (gt)
ABH = CDK (cmt)
Do đó, t/g ABH = t/g CDK ( cạnh huyền - góc nhọn)
=> AH = CK (2 cạnh tương ứng) (1)
Có: AH // A'B' ( cùng _|_ BB')
AA' // B'H ( cùng _|_ A'D')
=> AH = A'B' ( tính chất đoạn chắn) (2)
Tương tự ta cũng có: CK = C'D' (3)
Từ (1); (2) và (3) => A'B' = C'D' (đpcm)

Lời giải:
Ta có \(`\left\{\begin{matrix} \frac{a}{a'}+\frac{b'}{b}=1\\ \frac{b}{b'}+\frac{c'}{c}=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} ab+a'b'=a'b\\ bc+b'c'=b'c\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} ab=a'b-a'b'\\ b'c'=b'c-bc\end{matrix}\right.\Rightarrow \left\{\begin{matrix} abc=a'bc-a'b'c\\ a'b'c'=a'b'c-a'bc\end{matrix}\right.\)
\(\Rightarrow abc+a'b'c'=0\)
Do đó ta có đpcm.

a: \(=\dfrac{1}{4}\cdot4-\dfrac{3}{4}\cdot\dfrac{4}{5}=1-\dfrac{3}{5}=\dfrac{2}{5}\)

b) \(\frac{26+x}{39-x}=\frac{6}{7}\)
=> 7( 26+ x) = 6(39-x)
=>182 +7x = 234 - 6x
=> 7x+6x = 234-182
=> 13x= 52
=> x=4
a) \(\frac{26+x}{39+x}=\frac{6}{7}\)
=> 7(26+x) = 6(39+x)
=> 182 + 7 x = 234 + 6x
=> 7x - 6x = 234 - 182
=> x = 52

- Điều này trái với tiên đề Ơ-clit vì M nằm ngoài đường thẳng d mà ta vừa có d'//d và d''//d, như vậy là qua một điểm M nằm ngoài đường thẳng d ta có hai đường thẳng song song với d.
- Vậy d' không thể cắt d'' => d'//d''.

1) Ta có: Oz nằm giữa tia Ox và Oy
\(\Rightarrow\widehat{xOz}=\widehat{xOy}-\widehat{yOz}=120^0-30^0=90^0\)
=> Oz⊥Ox
2) Ta có: Ox' là tia đối của tia Ox
\(\Rightarrow\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-120^0=60^0\)(2 góc kề bù)
Ta có: Ox' là tia đối của tia Ox, Oy' là tia đối của tia Oy
\(\widehat{\Rightarrow x'Oy'}=\widehat{xOy}=120^0\)(2 góc đối đỉnh)
1: Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOx}\)
nên tia Oz nằm giữa hai tia Ox và Oy
Suy ra: \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{xOz}=90^0\)
hay Ox\(\perp\)Oz

Lời giải:
Trên tia đối tia $MA$ lấy $D$ sao cho $MD=MA$
Dễ cm $\triangle BMA=\triangle CMD$ (c.g.c)
$\Rightarrow \widehat{MBA}=\widehat{MCD}$
Mà 2 góc này so le trong nên $BA\parallel CD$
$\Rightarrow CD\perp AC$ hay $\widehat{DCA}=90^0$
Cùng từ 2 tam giác bằng nhau trên suy ra $BA=CD$
Xét tam giác $BAC$ và $DCA$ có:
$BA=DC$
$\widehat{BAC}+\widehat{DCA}=90^0$
$AC$ chung
$\Rightarrow BC=DA$
Mà $DA=2AM$ nên $BC=2AM$

Hình vẽ:
Giải:
a) Đường thẳng a có vuông góc với đường thẳng d'. Vì đường thẳng a vuông góc với đường thẳng d, mà đường thẳng d song song với đường thẳng d'.
b) Đường thẳng a có vuông góc với đường thẳng d''. Vì đường thẳng a vuông góc với đường thẳng d, mà đường thẳng d song song với đường thẳng d''.
a) Đường thẳng d' có song song với đường thẳng d''. Vì đường thẳng d và đường thẳng d đều vuông góc với đường thẳng a (theo câu a, b).
Chúc bạn học tốt!
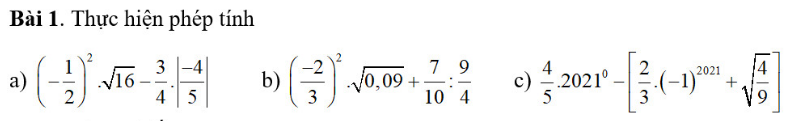



Bạn chỉ cần đọc như thường thôi, dấu '' // '' này thì bạn đọc là song song
d đọc là đê, d' đọc là đê phẩy, d" đọc là đê phẩy phẩy
Cho xin 1 tick