Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

a)
Sửa đề: ΔBIM=ΔCKM
Xét ΔBIM vuông tại I và ΔCKM vuông tại K có
BM=CM(M là trung điểm của BC)
\(\widehat{IBM}=\widehat{KCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBIM=ΔCKM(cạnh huyền-góc nhọn)

a) Xét ΔABM và ΔACM có
AB=AC(ΔABC cân tại A)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
\(a,\) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (giả thiết)
\(AM\) là cạnh chung
\(BM=CM\) (giả thiết)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
\(b,\) Vì \(\Delta ABM=\Delta ACM\) (chứng minh câu \(a\))
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) (\(2\) góc tương ứng)
\(\Rightarrow AM\) là tia phân giác \(\widehat{BAC}\)
\(c,\) Vì \(\Delta ABC\) cân tại \(A\) (giả thiết)
Mà \(AM\) là tia phân giác \(\widehat{BAC}\) (chứng minh câu \(b\))
\(\Rightarrow AM\) là đường trung trực \(\Delta ABC\)
\(\Rightarrow AM\perp BC\) tại \(M\)

Căng =))) Mà chỉ biết làm nếu có đường trung tuyến thôi âydaaa
Thôi để người khác làm nhé
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!

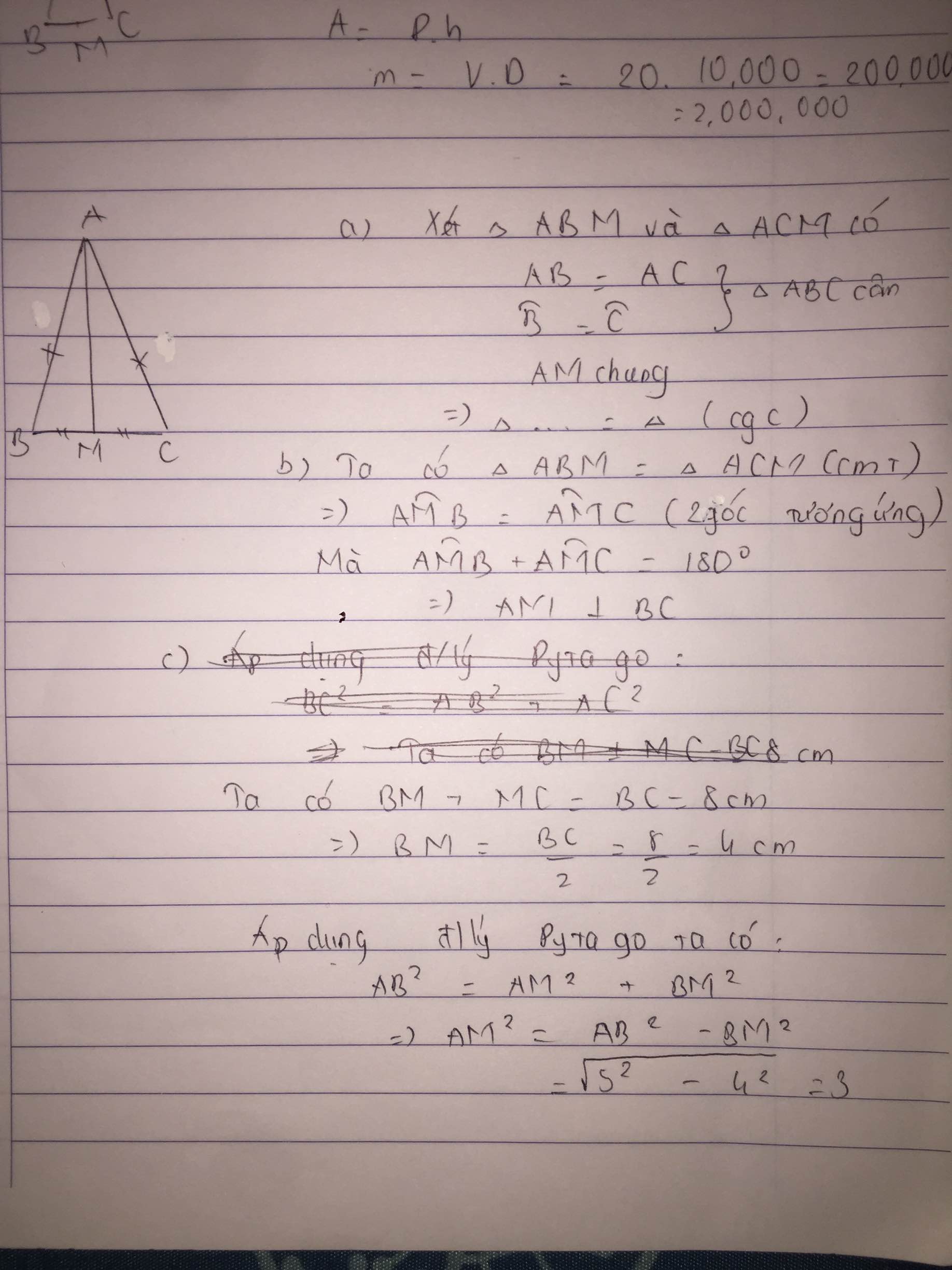
Lời giải:
Trên tia đối tia $MA$ lấy $D$ sao cho $MD=MA$
Dễ cm $\triangle BMA=\triangle CMD$ (c.g.c)
$\Rightarrow \widehat{MBA}=\widehat{MCD}$
Mà 2 góc này so le trong nên $BA\parallel CD$
$\Rightarrow CD\perp AC$ hay $\widehat{DCA}=90^0$
Cùng từ 2 tam giác bằng nhau trên suy ra $BA=CD$
Xét tam giác $BAC$ và $DCA$ có:
$BA=DC$
$\widehat{BAC}+\widehat{DCA}=90^0$
$AC$ chung
$\Rightarrow BC=DA$
Mà $DA=2AM$ nên $BC=2AM$
Hình vẽ:
