K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
2
25 tháng 8 2021
1) Ta có: Oz nằm giữa tia Ox và Oy
\(\Rightarrow\widehat{xOz}=\widehat{xOy}-\widehat{yOz}=120^0-30^0=90^0\)
=> Oz⊥Ox
2) Ta có: Ox' là tia đối của tia Ox
\(\Rightarrow\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-120^0=60^0\)(2 góc kề bù)
Ta có: Ox' là tia đối của tia Ox, Oy' là tia đối của tia Oy
\(\widehat{\Rightarrow x'Oy'}=\widehat{xOy}=120^0\)(2 góc đối đỉnh)
25 tháng 8 2021
1: Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOx}\)
nên tia Oz nằm giữa hai tia Ox và Oy
Suy ra: \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{xOz}=90^0\)
hay Ox\(\perp\)Oz
LT
1
24 tháng 1 2022
Xét tứ giác MECF có
ME//CF
MF//EC
Do đó: MECF là hình bình hành
Suy ra: ME=CF, MF=EC
ME+MF=CF+EC ko đổi
20 tháng 11 2021
Câu 22:
Có.Vì \(1.15=3.5\left(=15\right)\) nên ta có thể lập tỉ lệ thức từ các số đã cho
VD:\(\dfrac{1}{3}=\dfrac{5}{15}\)
Câu 23:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=-5.7=-35\end{matrix}\right.\)
Vậy....
AH
Akai Haruma
Giáo viên
27 tháng 10 2021
Lời giải:
Trên tia đối tia $MA$ lấy $D$ sao cho $MD=MA$
Dễ cm $\triangle BMA=\triangle CMD$ (c.g.c)
$\Rightarrow \widehat{MBA}=\widehat{MCD}$
Mà 2 góc này so le trong nên $BA\parallel CD$
$\Rightarrow CD\perp AC$ hay $\widehat{DCA}=90^0$
Cùng từ 2 tam giác bằng nhau trên suy ra $BA=CD$
Xét tam giác $BAC$ và $DCA$ có:
$BA=DC$
$\widehat{BAC}+\widehat{DCA}=90^0$
$AC$ chung
$\Rightarrow BC=DA$
Mà $DA=2AM$ nên $BC=2AM$
18 tháng 2 2022
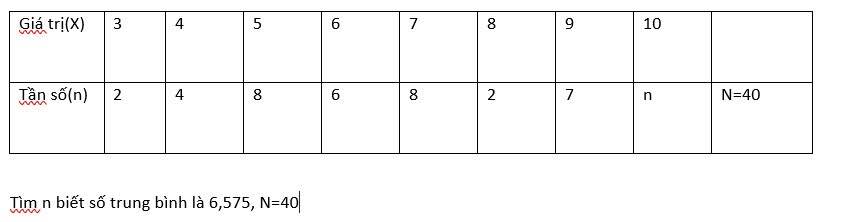
Có :\(\dfrac{3.2+4.4+5.8+6.6+7.8+8.2+9.7+10n}{40}=6,575\)
\(6+16+40+36+56+16+63+10n=263\)
233 + 10n =263
10n=30
n=3
hoặc 1 cách đơn giản hơn là :
2 + 4+8+6+8+2+7+n=40
37+n=40
n=3
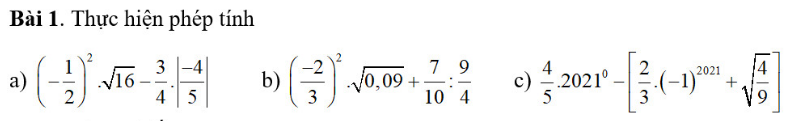
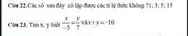
a: \(=\dfrac{1}{4}\cdot4-\dfrac{3}{4}\cdot\dfrac{4}{5}=1-\dfrac{3}{5}=\dfrac{2}{5}\)