Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn ơi cái này là 2 cạnh góc vuông hay là một cạch gv 1 cạnh huyeeng bn

Gọi x,y,zx,y,z là các cạnh của tam giác vuông (1≤x≤y<z)(1≤x≤y<z). Ta có :
x2+y2=z2(1)x2+y2=z2(1)
xy=2(x+y+z)(2)xy=2(x+y+z)(2)
Từ (1)(1) ta có :
z2=(x+y)2−2xy=(x+y)2−4(x+y+z)⇒(x+y)2−4(x+y)+4=z2−4z+4z2=(x+y)2−2xy=(x+y)2−4(x+y+z)⇒(x+y)2−4(x+y)+4=z2−4z+4
⇒(x+y−2)2=(z+2)2⇒(x+y−2)2=(z+2)2
⇒x+y−2=z+2(x+y≥2)⇒x+y−2=z+2(x+y≥2)
Thay z=x+y−4z=x+y−4 vào (2)(2) ta được :
(x−4)(y−4)=8(x−4)(y−4)=8
⇔x−4=1;y−4=8⇔x−4=1;y−4=8 hoặc x−4=2;y−4=4x−4=2;y−4=4
⇔x=5;y=12⇔x=5;y=12 hoặc x=6;y=8x=6;y=8
lalallalalallalalla mij k djd jfjfj fiiddi ididi iddiidid didiididid idid idid idi didi dit con me chung may cho chet vois ogs

Chắc chắn là đề bài sai rồi em
Đúng như đề em ghi thì a;b;c là số tự nhiên lớn hơn 9
Giả sử c là cạnh huyền, nghich đảo của c là \(\dfrac{1}{c}< 1\) làm sao bằng a hay b được?

Gọi chu vi tam giác CMN bằng p.
Tìm ý tưởng: p = BC + CD, hệ thức này gợi cho ta đến tính chất của đường tròn bàng tiếp (xem bài 2). Ở đây là đường tròn bàng tiếp góc C của ΔCMN.
Gọi B’, D’ lần lượt là các tiếp điểm của đường tròn bàng tiếp góc C của ΔCMN với đường kéo dài cạnh CM, CN.
Ta đã có, CB’ = CD’ = = CB = CD B’ B và D D’. Do đó, tâm đường tròn bàng tiếp góc C của tam giác CMN là điểm A.
Từ đó, .
Gọi chu vi tam giác CMN bằng p.
Tìm ý tưởng: p = BC + CD, hệ thức này gợi cho ta đến tính chất của đường tròn bàng tiếp (xem bài 2). Ở đây là đường tròn bàng tiếp góc C của ΔCMN.
Gọi B’, D’ lần lượt là các tiếp điểm của đường tròn bàng tiếp góc C của ΔCMN với đường kéo dài cạnh CM, CN.
Ta đã có, CB’ = CD’ = = CB = CD B’ B và D D’. Do đó, tâm đường tròn bàng tiếp góc C của tam giác CMN là điểm A.
Từ đó, .
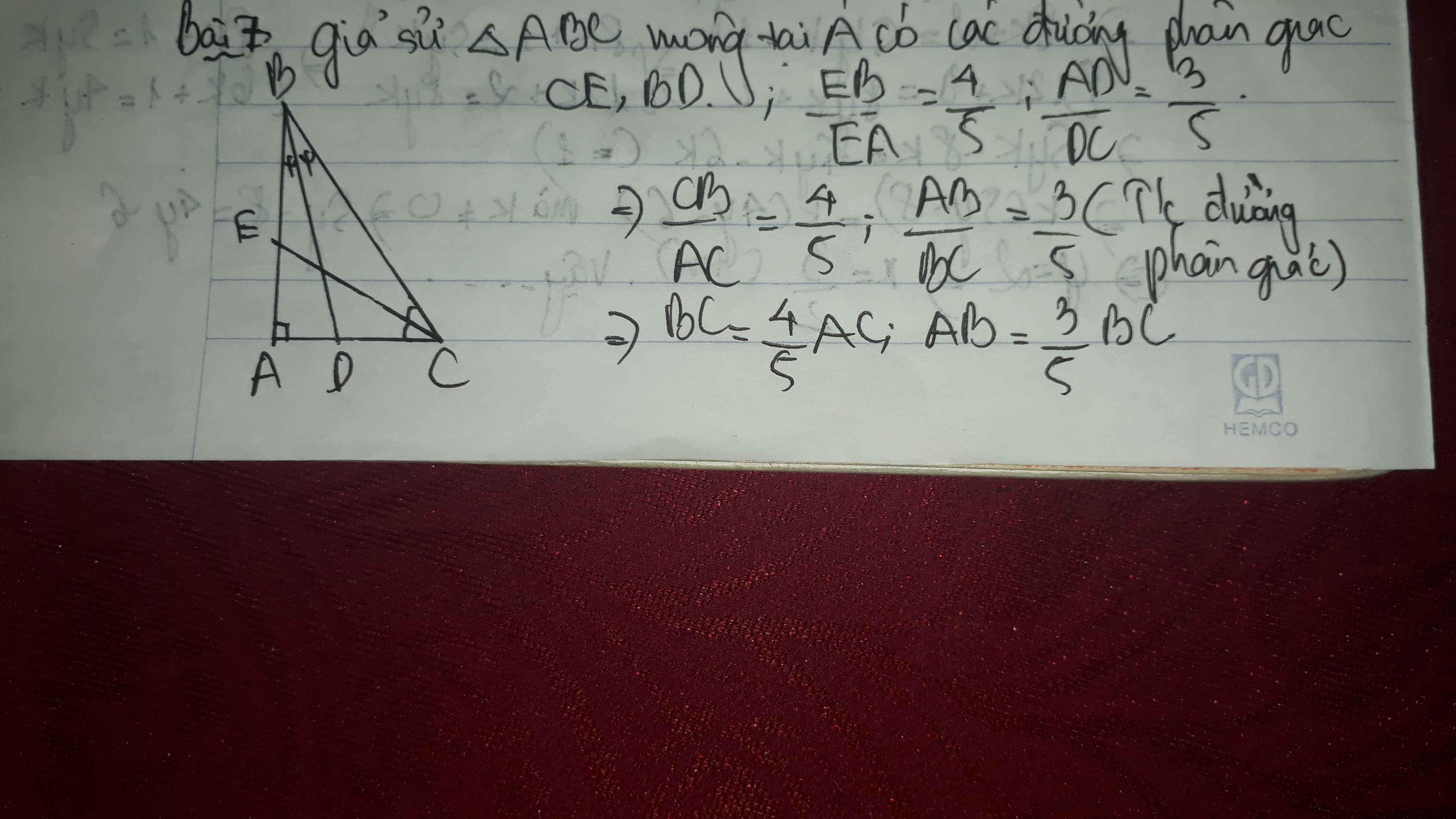
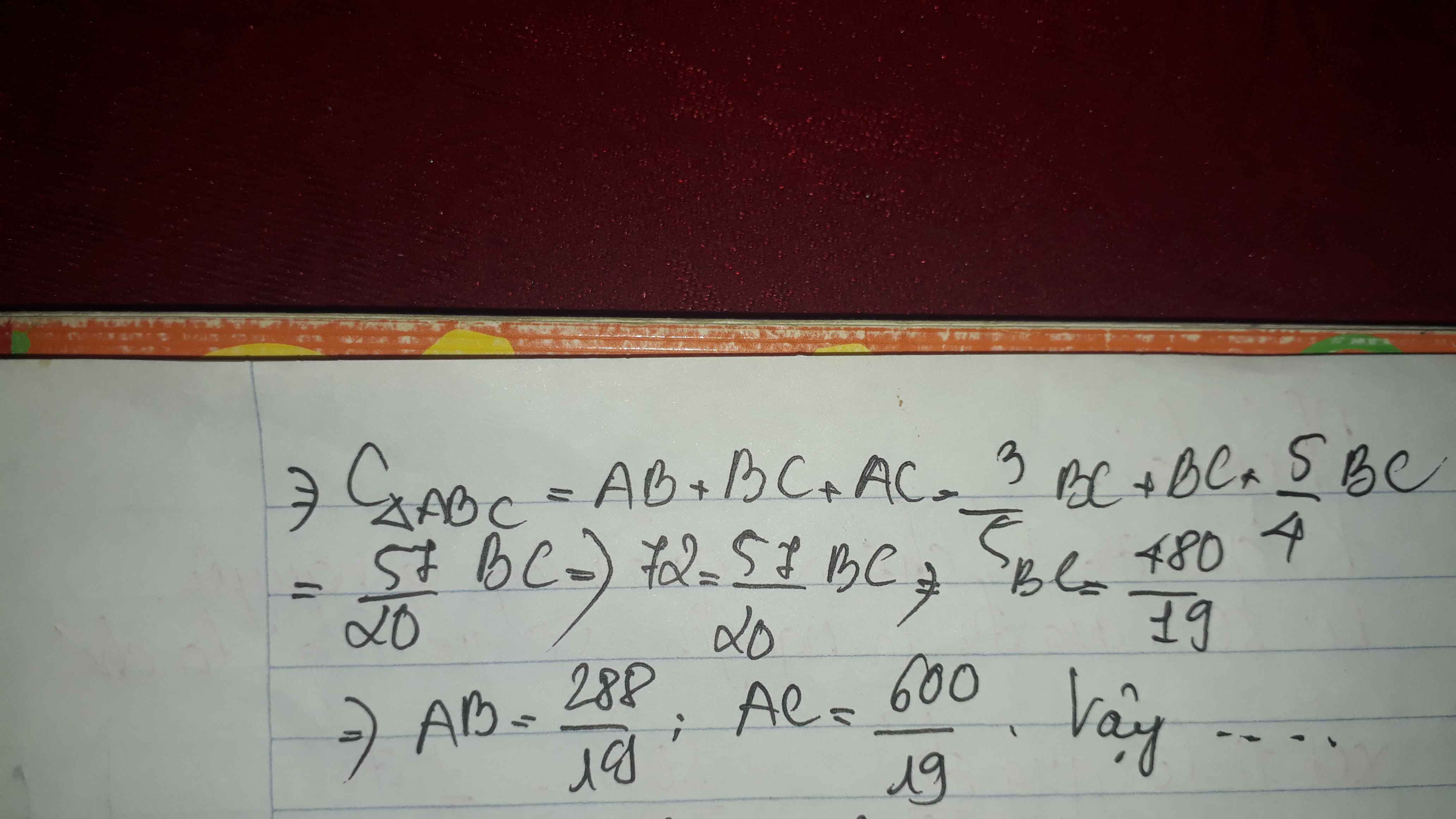
gọi 2 cạnh góc vuông lần lượt là a và b(a,b có vai trò như nhau;a,bϵ N)
thì độ dài cạnh huyền là\(\sqrt{a^2+b^2}\)
theo đề bài ta có: \(2.\frac{1}{2}a.b=3\left(a+b+\sqrt{a^2+b^2}\right)\)
→ab-3a-3b=3\(\sqrt{a^2+b^2}\)
→\(a^2b^2+9a^2+9b^2-6a^2b-6ab^2+18ab=9a^2+9b^2\)
→\(a^2b^2-6a^2b-6ab^2+18ab=0\)
→ab-6a-6b+18=0→(a-6)(b-6)=18=1.18=2.9=3.6(vì a,b>0→a-6;b-6>-6 nên ta loại các giá trị âm)
ta có bảng:
a-6 1 2 3
b-6 18 9 6
a 7 8 9
b 24 15 12
thử lại ta có tất cả đều t/m
vậy (a,b)ϵ\(\left\{\left(7,24\right);\left(8,15\right);\left(9,12\right)\right\}\)