Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với hình học bạn lưu ý chỉ nên đăng 1 bài 1 post. Đăng thế này khả năng bị bỏ qua bài rất cao, vì ai nhìn vào cũng thấy nản.

a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ
cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2
TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2 ÁP DỤNG PITA GO TÌM RA CẠNH bc
b,

Dễ ẹt;
Giả sử \(\Delta\)ABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên \(\left(\frac{BI}{AC}\right)=\left(\frac{BD}{DC}\right)=\left(\frac{BD}{3BD}\right)=\frac{1}{3}\) (định lí Ta lét)
mà BI=AB nên \(\frac{AB}{AC}=\frac{1}{3}\)
Cm \(\Delta\)AHC đồng dạng \(\Delta\)BHA(g.g) nên \(\frac{BH}{HA}=\frac{HA}{HC}=\frac{AB}{AC}=\frac{1}{3}\)
nên \(BH=\frac{1}{3}AH\);\(HC=3AH\)nên \(\frac{BH}{HC}=\frac{1}{9}\)

câu 2
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
(hình bạn tự vẽ nhé)
Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5

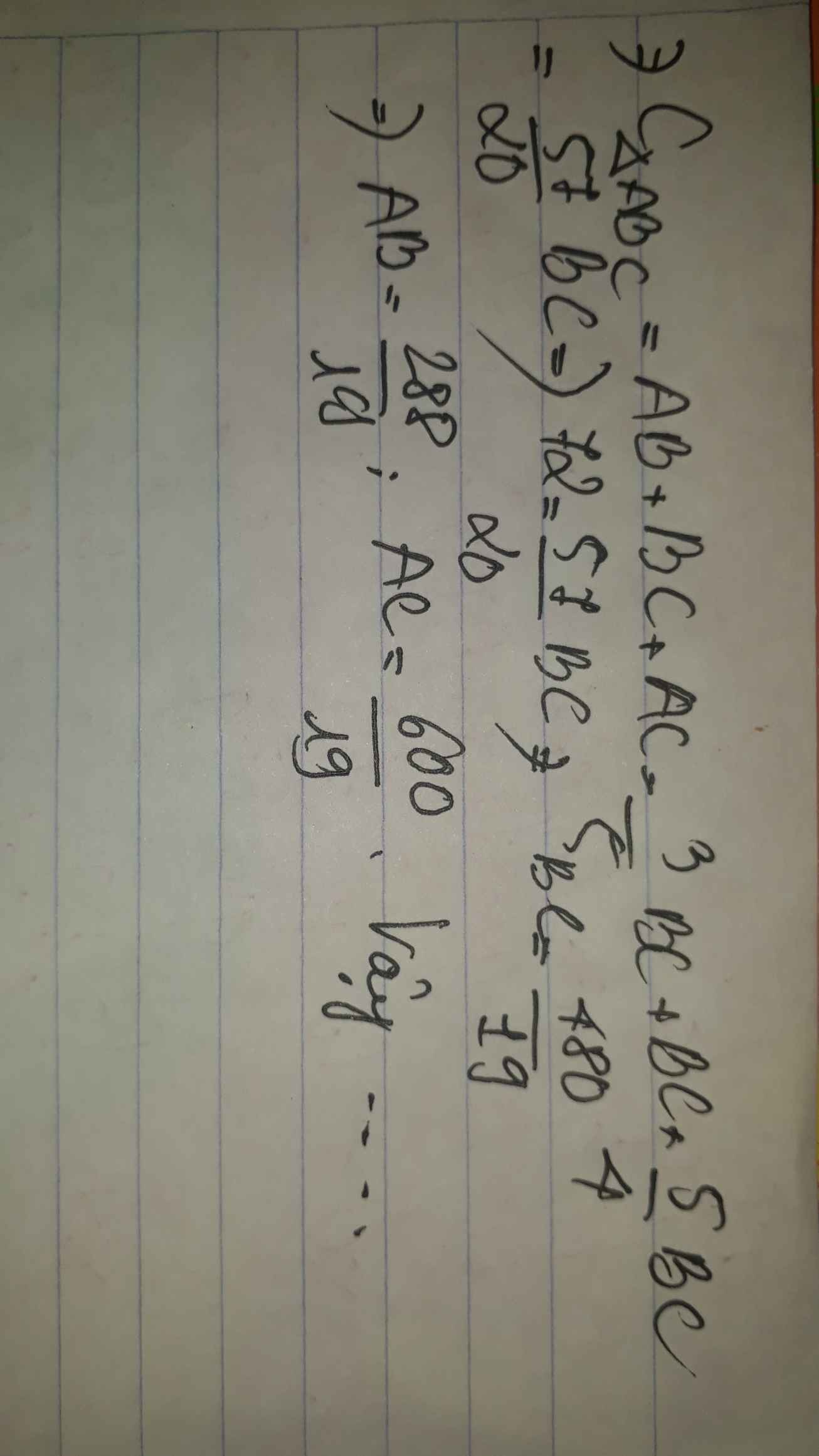
Bài 7:
cảm ơn anh nhiều