Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\left(\frac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}-\frac{1}{\sqrt{x}+1}\right).\frac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}\)
\(B=\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}.\frac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}\)
\(B=\frac{-\sqrt{x}-1}{\sqrt{x}}\). Vậy ....

a, \(B=\frac{\sqrt{x}-1}{\sqrt{x}}+\frac{2\sqrt{x}+1}{x+\sqrt{x}}\) (ĐKXĐ: \(x>0\))
\(=\frac{\sqrt{x}-1}{\sqrt{x}}+\frac{2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)+2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{x-1+2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{\sqrt{x}+2}{\sqrt{x}+1}\)
b, \(\frac{A}{B}=\frac{2+\sqrt{x}}{\sqrt{x}}:\frac{\sqrt{x}+2}{\sqrt{x}+1}=\frac{\sqrt{x}+1}{\sqrt{x}}\)
\(\frac{A}{B}>\frac{3}{2}\Leftrightarrow\frac{\sqrt{x}+1}{\sqrt{x}}-\frac{3}{2}>0\)
\(\Leftrightarrow\frac{2\sqrt{x}+2-3\sqrt{x}}{2\sqrt{x}}>0\)
\(\Leftrightarrow2-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 2\Leftrightarrow x< 4\)
Kết hợp với điều kiện \(x>0\)ta có: \(0< x< 4\)
Vậy với \(0< x< 4\)thì \(\frac{A}{B}>\frac{3}{2}\)

a) (Tự giải) ĐKXĐ: \(x\ge0;x\ne4;x\ne9\)
b) \(Q=\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\frac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\frac{\sqrt{x}-3}{\sqrt{x}-2}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\frac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{\sqrt{x}-3+4}{\sqrt{x}-3}=1-\frac{4}{\sqrt{x}-3}\)
c) Để Q là 1 số nguyên => \(1-\frac{4}{\sqrt{x}-3}\in Z\)
Mà \(1\in Z\Rightarrow\frac{4}{\sqrt{x}-3}\in Z\)
=> \(4⋮\sqrt{x}-3\)
Hay \(\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
ta lập bảng
| \(\sqrt{x}-3\) | 1 | -1 | 2 | -2 | 4 | -4 |
| x | 16 (TM) | 4 (KTM) | 25 (TM) | 1(TM) | 49(TM) | vô lý |
Vậy x={1;16;25;49}

a) ĐK: a > 0; b > 0
\(A=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\frac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}-b\)
\(=\frac{\sqrt{a}+\sqrt{b}+2\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\frac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}-b\)
\(=\frac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}-\left(\sqrt{a}-\sqrt{b}\right)-b\)
\(=\sqrt{a}+\sqrt{b}-\sqrt{a}+\sqrt{b}-b\)
\(=2\sqrt{b}-b\)
b) \(A=1\)\(\Rightarrow\)\(2\sqrt{b}-b=1\)
\(\Leftrightarrow\)\(b-2\sqrt{b}+1=0\)
\(\Leftrightarrow\) \(\left(\sqrt{b}-1\right)^2=0\)
\(\Leftrightarrow\)\(\sqrt{b}-1=0\)
\(\Leftrightarrow\)\(\sqrt{b}=1\)
\(\Leftrightarrow\)\(b=1\) (t/m ĐKXĐ)
Vậy b=1

=\(\left(\frac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{x-9}\right)\):\(\left(\frac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\right)\)
=\(\left(\frac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{x-9}\right)\):\(\left(\frac{\sqrt{x}+1}{\sqrt{x}-3}\right)\)=\(\frac{-3\left(\sqrt{x}+1\right)}{x-9}\).\(\frac{\sqrt{x}-3}{\sqrt{x}+1}\)
=\(\frac{-3}{\sqrt{x}+3}\)

Lời giải:
$\frac{5n+2}{2n+1}=\frac{2,5(2n+1)-0,5}{2n+1}=2,5-\frac{0,5}{2n+1}$
Để $\frac{5n+2}{2n+1}$ lớn nhất thì $\frac{0,5}{2n+1}$ nhỏ nhất
$\Leftrightarrow 2n+1$ lớn nhất
$\Leftrightarrow n$ lớn nhất. Trong tập số tự nhiên thì không tồn tại số tự nhiên lớn nhất nên không có GTLN
Để $\frac{5n+2}{2n+1}$ nhỏ nhất thì $\frac{0,5}{2n+1}$ lớn nhất
$\Leftrightarrow 2n+1$ nhỏ nhất $\Leftrightarrow n$ nhỏ nhất
Với $n\in\mathbb{N}^*$ thì $n$ nhỏ nhất bằng $1$
$\Rightarrow \frac{5n+2}{2n+1}$ min $=\frac{5.1+2}{2.1+1}=\frac{7}{3}$
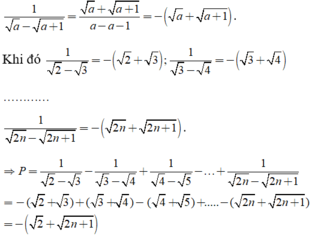
a) 10n + 1 - 6.10n
= 10n . 10 - 6 . 10n
= 10n . (10 - 6)
= 10n . 4
b) 2n + 3 + 2n + 2 - 2n + 1 + 2n
= 2n . 23 + 2n . 22 - 2n . 2 + 2n . 1
= 2n . (8 + 4 - 2 + 1)
= 2n . 11