Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện : x> 0
Ta có 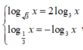
, khi đó phương trình đã cho trở thành
( log3x)2 - 4log3x+ 2log3x-3= 0 hay ( log3x)2 - 2log3x- 3= 0 (*)
Đặt t= log3x, suy ra phương trình (*) trở thành : t2- 2t-3= 0
Suy ra t= -1 hoặc t= 3
Với t= -1, ta được ![]()
Với t= 3 ta được log3x= 3 nên x2= 27
Từ đó ; P= log3x1+ log27x2 = log3 + log2727 = -1+ 1= 0
Chọn A

\(ĐK:x>2\\ Pt\Leftrightarrow\log_3\left(x-2\right)^2\left(x-4\right)^2=0\\ \Leftrightarrow\left(x-2\right)^2\left(x-4\right)^2=1\Leftrightarrow\left[{}\begin{matrix}x^2-6x+9=0\\x^2-6x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\3+\sqrt{2}\end{matrix}\right.\)
\(\left(x_1-x_2\right)^2=\left(\sqrt{2}+3-3\right)^2=2\)

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
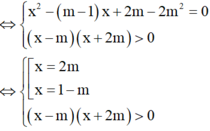
Điều kiện để pt đã cho có 2 nghiệm
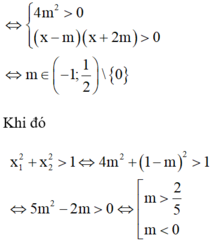
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Đáp án A
Ghi nhớ: Nếu hàm số ![]()
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]()
có ít nhất một nghiệm nằm trong khoảng ![]() .
.

Đáp án D
Phương pháp:
Đặt 2x = t, t > 0. Chuyển về bài toán tìm m để phương trình bậc 2 ẩn t có 2 nghiệm t1, t2 thỏa mãn t1.t2 = 8
Cách giải:

Để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 thì phương trình (2) có 2 nghiệm t1,t2 thỏa mãn t1.t2 = 2x1.2x2 = 2x1 + x2 = 23 = 8
Khi đó:
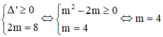

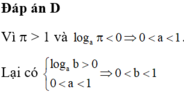

Chọn A.
Điều kiện. x > 0
Ta có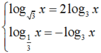 , khi đó phương trình đã cho trở thành
, khi đó phương trình đã cho trở thành
( log3x) 2 - 4log3x + 2log3x - 3 = 0 hay ( log3x) 2 - 2log3x – 3 = 0 (*)
Đặt t = log3x, suy ra phương trình (*) trở thành : t2 - 2t – 3 = 0
Suy ra t = -1 hoặc t = 3
Với t = -1, ta được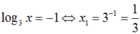
Với t = 3 ta được log3x = 3 hay x2 = 27
Từ đó : P = log3x1 + log27x2 = 0.