Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Điều kiện. x > 0
Ta có 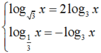 , khi đó phương trình đã cho trở thành
, khi đó phương trình đã cho trở thành
( log3x) 2 - 4log3x + 2log3x - 3 = 0 hay ( log3x) 2 - 2log3x – 3 = 0 (*)
Đặt t = log3x, suy ra phương trình (*) trở thành : t2 - 2t – 3 = 0
Suy ra t = -1 hoặc t = 3
Với t = -1, ta được 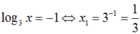
Với t = 3 ta được log3x = 3 hay x2 = 27
Từ đó : P = log3x1 + log27x2 = 0.

Chọn D.
Điều kiện : x> 0
Ta có
![]() và đặt t = log27x
và đặt t = log27x
Khi đó, phương trình đã cho trở thành
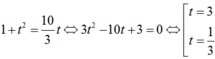
Với t = 3, ta được log27x = 3 nên x = 39
Với t = 1/3 , ta được
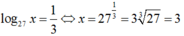
Theo đề bài ra, ta có
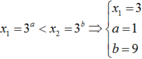
![]()

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
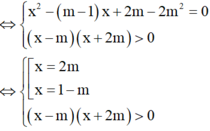
Điều kiện để pt đã cho có 2 nghiệm
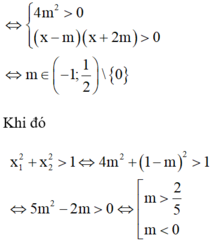
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Chọn A.
Điều kiện: ![]()
Phương trình
![]()
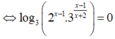
![]()
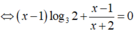
![]()
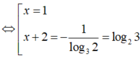
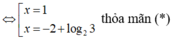
Do đó S = -1 + log23 = log23 – log22 = log23/2.

Chọn C.
Điều kiện:
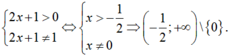 .
.
Đặt t = log3(2x + 1) suy ra
![]()
Khi đó, phương trình đã cho trở thành
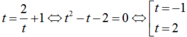
Với t = -1 ta có log3( 2x + 1) = -1 hay 2x + 1 = 3-1 nên x = -1/3
Với t = 2 ta có log3(2x + 1) = 2 hay 2x + 1 = 32 nên x = 4
Vậy giá trị biểu thức ![]()

Chọn B.
Phương trình đã cho tương đương với: x2- 4x+2= x-4 hay x2- 5x + 6= 0
Từ đó; x= 2 hoặc x= 3
Do đó: S= 24+ 34= 97
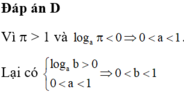
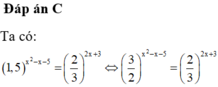
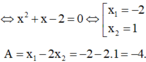

Điều kiện : x> 0
Ta có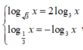
, khi đó phương trình đã cho trở thành
( log3x)2 - 4log3x+ 2log3x-3= 0 hay ( log3x)2 - 2log3x- 3= 0 (*)
Đặt t= log3x, suy ra phương trình (*) trở thành : t2- 2t-3= 0
Suy ra t= -1 hoặc t= 3
Với t= -1, ta được
Với t= 3 ta được log3x= 3 nên x2= 27
Từ đó ; P= log3x1+ log27x2 = log3 + log2727 = -1+ 1= 0
Chọn A