Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Điều kiện:
.
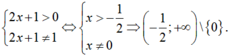Đặt t = log3(2x + 1) suy ra
Khi đó, phương trình đã cho trở thành
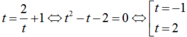
Với t = -1 ta có log3( 2x + 1) = -1 hay 2x + 1 = 3-1 nên x = -1/3
Với t = 2 ta có log3(2x + 1) = 2 hay 2x + 1 = 32 nên x = 4
Vậy giá trị biểu thức 
Đáp án D.
ĐK: x > 2.
TH1: Ta thấy x = 3 không phải là nghiệm của PT.
TH2: Với x ≠ 3 logarit cơ số x – 2 cả 2 vế ta được
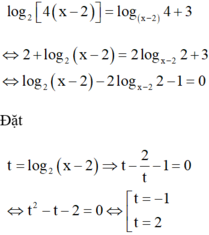
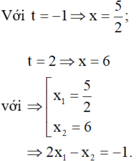
Chọn A.
Điều kiện: 
Phương trình
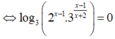
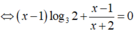
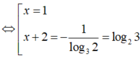
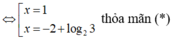
Do đó S = -1 + log23 = log23 – log22 = log23/2.
Chọn A.
Điều kiện. x > 0
Ta có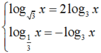 
, khi đó phương trình đã cho trở thành
( log3x) 2 - 4log3x + 2log3x - 3 = 0 hay ( log3x) 2 - 2log3x – 3 = 0 (*)
Đặt t = log3x, suy ra phương trình (*) trở thành : t2 - 2t – 3 = 0
Suy ra t = -1 hoặc t = 3
Với t = -1, ta được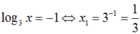 
Với t = 3 ta được log3x = 3 hay x2 = 27
Từ đó : P = log3x1 + log27x2 = 0.
Chọn D.
Phương trình 
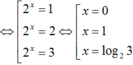thỏa mãn (*)
Do đó S = 1+ log23 = log26.
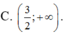
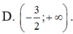
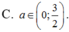
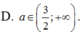
\(ĐK:x>2\\ Pt\Leftrightarrow\log_3\left(x-2\right)^2\left(x-4\right)^2=0\\ \Leftrightarrow\left(x-2\right)^2\left(x-4\right)^2=1\Leftrightarrow\left[{}\begin{matrix}x^2-6x+9=0\\x^2-6x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\3+\sqrt{2}\end{matrix}\right.\)
\(\left(x_1-x_2\right)^2=\left(\sqrt{2}+3-3\right)^2=2\)