Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(v^2-v_0^2=2gh\)
=> \(v=\sqrt{2gh+v_0^2}=\sqrt{2.10.10+10^2}=10\sqrt{m}\left(\dfrac{m}{s}\right)\)

Vì vật rơi nhanh dần đều từ độ cao h = 10 m xuống đất với vận tốc đầu v 0 = 6 m/s và gia tốc g = 9,8 m/ s 2 , nên ta có:
v 2 - v 0 2 = 2gh
Suy ra vận tốc ngay trước khi chạm đất bằng:


Khi vật đạt độ cao cực đại \(\Leftrightarrow v=0\)
\(\Rightarrow W=W_t\\ \Leftrightarrow mgh+mv^2=mgh_{max}\\ \Leftrightarrow120=mgh_{max}\\ \Leftrightarrow h_{max}=\dfrac{120}{mg}=\dfrac{120}{2.10}=6\left(m\right)\)

a)
Cơ năng tại O (vị trí ném): \(W_o=\dfrac{1}{2}mv_o^2+mgz_o\)
Cơ năng tại B (mặt đất): \(W_B=\dfrac{1}{2}mv_B^2\)
Áp dụng định luật bảo toàn cơ năng tại O và A ta có:
\(W_O=W_B\Leftrightarrow\) \(\dfrac{1}{2}mv_O^2+mgz_o=\dfrac{1}{2}mv_B^2\Leftrightarrow v_O^2=2gh\Rightarrow h=\dfrac{v_B^2-v_O^2}{2g}=25m\)
b) Khi đạt độ cao cực đại thì vtoc vật = 0
\(\Leftrightarrow\dfrac{1}{2}mv_B^2=mgh_{cđ}\Leftrightarrow h_{cđ}=\dfrac{v_B^2}{2g}=45m\)
c) \(W_đ=W_t\Leftrightarrow W_đ=\dfrac{1}{2}W_B\Leftrightarrow\dfrac{1}{2}mv^2=\dfrac{1}{2}.\dfrac{1}{2}mv_B^2\Leftrightarrow v=10\sqrt{2}\left(\dfrac{m}{s}\right)\)

Chọn đáp án C
Chọn gốc tọa độ tại mặt đất, chiều dương hướng lên.
Phương trình vận tốc là

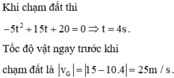
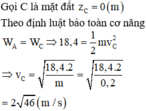
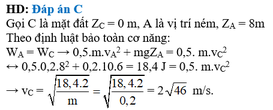
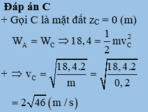

Vận tốc vật ngay trước khi chạm đất:
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot15}=10\sqrt{3}\)m/s