ngày THI ĐẤU OLM tối nay, ngày 28/04/2023 để so tài với học sinh toàn quốc!!!

Ôn tập kiểm tra học kì 2 hiệu quả, đạt thành tích cao!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
SL
Sakura Linh
22 tháng 9 2016

Kéo con lắc cho dây treo hợp với phương đứng 1 góc 19 độ rồi thả dao động điều hòa. Tính Vmax? Tính sức căng dây ở VTCB?
#Vật lý lớp 12
1
LC
Linh Cao
22 tháng 9 2016

Tham khảo:

/hoi-dap/question/93772.html?auto=1

 

Đúng(0)
NP
Nguyễn Phương Thảo
7 tháng 5 2016
 Một con lắc đơn có chu kì dđ là T=2s,vật nặng khối lượng m=500g.Dđ điều hoà tại nơi có g=10m/s^2 . Treo con lắc đơn vào trần nhà 1 toa xe đang chuyển động nhanh dần đều trên mặt đường nằm ngang thì thấy rằng ở VTCB mới,dây treo con lắc hợp với phương 1 góc α=30 độ .Từ VTCB kéo con lắc lệch khỏi phương 1 góc 40 độ rồi thả nhẹ. Vận tốc của con lắc khi đi qua VTCB là??Ai giải hộ...
Đọc tiếp

 Một con lắc đơn có chu kì dđ là T=2s,vật nặng khối lượng m=500g.Dđ điều hoà tại nơi có g=10m/s^2 . Treo con lắc đơn vào trần nhà 1 toa xe đang chuyển động nhanh dần đều trên mặt đường nằm ngang thì thấy rằng ở VTCB mới,dây treo con lắc hợp với phương 1 góc α=30 độ .Từ VTCB kéo con lắc lệch khỏi phương 1 góc 40 độ rồi thả nhẹ. Vận tốc của con lắc khi đi qua VTCB là??

Ai giải hộ với??
#Vật lý lớp 12
2
NT
Nguyễn Thế Vinh
8 tháng 5 2016

leuleu

Đúng(0)
NP
Nguyễn Phương Thảo
8 tháng 5 2016

Nếu b biết giải bài này thì chỗ kia là hợp với phương thẳng đứng 40 độ nha.

Đúng(0)
HD
Hoàng Đức Long
2 tháng 10 2017
Một toa xe trượt không ma sát trên một đường dốc xuống dưới, góc nghiêng của dốc so với mặt phẳng nằm ngang là 450. Lấy gia tốc trọng trường g = 10 m/s2. Treo lên trần toa xe một con lắc đơn gồm dây treo chiều dài 1,5 (m) nối với một quả cầu nhỏ. Trong thời gian xe trượt xuống, chu kì dao động nhỏ của con lắc đơn là A. 2,89 s B. 2,05 s C. 2,135 s D. 1,61...
Đọc tiếp

Một toa xe trượt không ma sát trên một đường dốc xuống dưới, góc nghiêng của dốc so với mặt phẳng nằm ngang là 450. Lấy gia tốc trọng trường g = 10 m/s2. Treo lên trần toa xe một con lắc đơn gồm dây treo chiều dài 1,5 (m) nối với một quả cầu nhỏ. Trong thời gian xe trượt xuống, chu kì dao động nhỏ của con lắc đơn là

A. 2,89 s

B. 2,05 s

C. 2,135 s

D. 1,61 s
#Vật lý lớp 12
1
VT
Vũ Thành Nam
2 tháng 10 2017

Đúng(0)
HD
Hoàng Đức Long
11 tháng 12 2018
Một chiếc xe trượt từ đỉnh dốc xuống chân dốc. Dốc nghiêng 30° so với phương ngang. Biết hệ số ma sát giữa xe và mặt dốc là 0,1. Lấy g = 10 m/s2. Một con lắc đơn có chiều dài dây treo 0,5 m được treo trong xe. Từ vị trí cân bằng của con lắc trong xe, kéo con lắc về hướng ngược chiều chuyển động của xe sao cho dây treo con lắc đơn hợp với phương thẳng đứng góc 30° rồi thả nhẹ. Trong...
Đọc tiếp

Một chiếc xe trượt từ đỉnh dốc xuống chân dốc. Dốc nghiêng 30° so với phương ngang. Biết hệ số ma sát giữa xe và mặt dốc là 0,1. Lấy g = 10 m/s2. Một con lắc đơn có chiều dài dây treo 0,5 m được treo trong xe. Từ vị trí cân bằng của con lắc trong xe, kéo con lắc về hướng ngược chiều chuyển động của xe sao cho dây treo con lắc đơn hợp với phương thẳng đứng góc 30° rồi thả nhẹ. Trong quá trình dao động của con lắc (xe vẫn trượt trên dốc), tốc độ cực đại của con lắc so với xe gần giá trị nào nhất sau đây?

 A. 0,33 m/s.

 B. 0,21 m/s.

 C. 1,2 m/s.

 D. 0,12 m/s.
#Vật lý lớp 12
1
VT
Vũ Thành Nam
11 tháng 12 2018

Đáp án B

Trước hết ta tìm gia tốc a  chuyển động của toa xe trên mặt phẳng nghiêng

Theo định luật II Niu-tơn  :

Xét theo phương Oy vuông góc với mặt phẳng nghiêng :

Phản lực : N = mgcos α

Lực ma sát F =  μ N   =   μ m g cos α

Xét theo phương Ox của mặt phẳng nghiêng thì : 

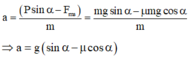
Với  β   =   90 0   -   α   ⇒ cos β   =   sin α , với F = ma

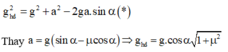
Chu kì dao động bé của con lắc đơn : T =  2 π 1 g hd   =   2 π 1 gcosα 1 + μ 2

Từ những dữ kiện trên ta thay số vào tính được :  v m a x   =   0 , 21   m / s

Đúng(0)
T
trầnchâu
28 tháng 6 2016

con lắc đơn có chiều dài l , khối lượng m =0,4kg , dao động điều hòa tại nơi có g=10m/s. biết sức căng của dây treo khi ở vị trí biên là 3 N thì sức căng của con lác khi qua VTCB là 
#Vật lý lớp 12
1
PT
༺ ๖ۣۜPhạm ✌Tuấn ✌Kiệτ ༻
28 tháng 6 2016

Áp dụng công thức T = mg (\(3\cos a-2\cos_{ }a_0\)) với a tại vị trí biên =a0 và T=3. ta tìm ra a0\(\approx0,23\pi\) 

thì sức căng của con lắc khi qua vị trí cân bằng là : T=mg (3-2cosa0)=6N

Đúng(0)
T
tranhoainina
11 tháng 9 2016

một con lắc đơn có chiều dài l. Kéo con lắc lệch khỏi vị trí cân bằng một góc \anpha_{0}= 30 độ rồi thả nhẹ cho dao động. Khi đi qua VTCB dây treo bị vướng vào 1 chiếc đinh nằm trên đường thẳng đứng cách điểm treo con lắc 1 đoạn l/2. Tính biên độ góc beta mà con lắc đạt được sau khi vướng đinh?
#Vật lý lớp 12
1
CT
Chú Tiểu
15 tháng 9 2016

Câu hỏi của Chivas Nguyễn - Vật lý lớp 12 | Học trực tuyến

Đúng(0)
HX
Hoa Xương Rồng
4 tháng 8 2016

một con lắc đơn dây dài l=1m dao động điều hòa với biên độ góc ampha(0)=4 .khi qua VTCB dây treo bị giữ lại ở 1 vị trí trên đường thẳng đứng,sau đó con lắc dao động với dây dài l' và biên độ góc  ampha'=8 .cơ năng của dao động sẽ:
#Vật lý lớp 12
1
TH
Trần Hoàng Sơn
4 tháng 8 2016

Khi vật qua VTCB thì động năng bằng cơ năng, nếu giữ dây treo tại 1 vị trí nào đó thì tốc độ của vật không đổi --> động năng không đổi

--> Cơ năng không thay đổi.

Chọn phương án B.

Đúng(0)
MD
Minh Đứcc
19 tháng 8 2016

1 quả cầu m=200g treo vào một dây dài l tạo thành 1 con lắc đơn , được đặt ở nơi có g=10m/s2 . Từ VTCB kéo cho dây lệch một góc α0 rồi buông nhẹ.Trong quá trình dao động lực căng dây bằng 1N.Tính góc tạo bởi dây treo và phương thẳng đứng tại vị trí thế năng bằng động năng, lực căng lúc này là bao nhiêu ?

 
#Vật lý lớp 12
2
TH
Trần Hoàng Sơn
20 tháng 8 2016

Lực căng dây cực tiểu tại vị trí biên:

\(T_{min}=mg(3.\cos\alpha_0-2\cos\alpha_0)=mg.\cos\alpha_0\)

\(\Rightarrow 0,2.10.\cos\alpha_0=1\)

\(\Rightarrow \alpha_0=60^0\)

Tại vị trí thế năng bằng động năng thì cơ năng là: \(W=W_t+W_đ=2W_t\)

\(\Rightarrow mgl(1-\cos\alpha_0)=2.mgl(1-\cos\alpha)\)

\(\Rightarrow \cos\alpha=\dfrac{1+\cos\alpha_0}{2}=\dfrac{3}{4}\)

\(\Rightarrow \alpha=41,4^0\)

Lực căng dây: \(T=mg(3\cos\alpha-2\cos\alpha_0)=0,2.10.(3.\dfrac{3}{4}-2.\dfrac{1}{2})=2,5(N)\)

Đúng(0)
TH
Trần Hoàng Sơn
20 tháng 8 2016

Lực căng dây: \(T=mg(3\cos \alpha-2\cos \alpha_0)\)

Lực căng dây cực đại ở VTCB: \(T_{max}=mg(3-2\cos \alpha_0)=1\)

\(\Rightarrow 0,2.10.(3-2\cos \alpha_0)=1\)

\(\Rightarrow \cos\alpha_0=\dfrac{5}{4}\), vô lý

Bạn xem lại đề nhé.

Đúng(0)
HD
Hoàng Đức Long
11 tháng 6 2018
Một con lắc đơn gồm một quả cầu nhỏ, khối lượng 100g treo vào trần nhà bằng một sợi dây dài 1m, ở nới có gia tốc trọng trường g = 9,8 m/s2. Bỏ qua mọi ma sát. Kéo vật nặng lệch một góc 300 rồi buông nhẹ. Tốc độ và lực căng dây tại vị trí dây treo hợp với phương thẳng đứng 100 là: A. 1,620 m/s; 0,586 N. B. 1,243 m/s; 1,243 N. C. 1,526 m/s; 1,198 N. D. 1,079 m/s; 0,616...
Đọc tiếp

Một con lắc đơn gồm một quả cầu nhỏ, khối lượng 100g treo vào trần nhà bằng một sợi dây dài 1m, ở nới có gia tốc trọng trường g = 9,8 m/s2. Bỏ qua mọi ma sát. Kéo vật nặng lệch một góc 300 rồi buông nhẹ. Tốc độ và lực căng dây tại vị trí dây treo hợp với phương thẳng đứng 100 là:

A. 1,620 m/s; 0,586 N.

B. 1,243 m/s; 1,243 N.

C. 1,526 m/s; 1,198 N.

D. 1,079 m/s; 0,616 N.
#Vật lý lớp 12
1
VT
Vũ Thành Nam
11 tháng 6 2018

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP