K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
2
1 tháng 1 2022
\(\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\left(\dfrac{a-1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{a-4}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\right)\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{3}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
2 tháng 9 2021
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)
DT
0
TT
2
3 tháng 11 2021
\(a,ĐK:-3x\ge0\Leftrightarrow x\le0\left(-3< 0\right)\\ b,ĐK:4-2x\ge0\Leftrightarrow-2x\ge-4\Leftrightarrow x\le2\\ c,ĐK:\dfrac{1}{2x-5}\ge0\Leftrightarrow2x-5>0\left(1>0;2x-5\ne0\right)\\ \Leftrightarrow x>\dfrac{5}{2}\\ d,ĐK:\dfrac{4x+7}{-3}\ge0\Leftrightarrow4x+7\le0\left(-3< 0\right)\Leftrightarrow x\le-\dfrac{7}{4}\)
TN
0
29 tháng 3 2021
a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
\(\Leftrightarrow sđ\stackrel\frown{AB}=60^0\)
15 tháng 8 2021
a: Ta có: AD=DE=EC
mà AD+DE+EC=3a
nên \(AD=DE=EC=a\)
mà AB=a
nên AB=AD=DE=EC=a và DC=2a
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=BA^2+AD^2\)
\(\Leftrightarrow BD^2=a^2+a^2=2a^2\)
hay \(BD=a\sqrt{2}\)
Ta có: \(\dfrac{DE}{DB}=\dfrac{a}{a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
mà \(\dfrac{DB}{DC}=\dfrac{a\sqrt{2}}{2a}=\dfrac{\sqrt{2}}{2}\)
nên \(\dfrac{DE}{DB}=\dfrac{DB}{DC}\)
b: Xét ΔBDE và ΔCDB có
\(\dfrac{DE}{DB}=\dfrac{DB}{DC}\)
\(\widehat{BDC}\) chung
Do đó: ΔBDE\(\sim\)ΔCDB
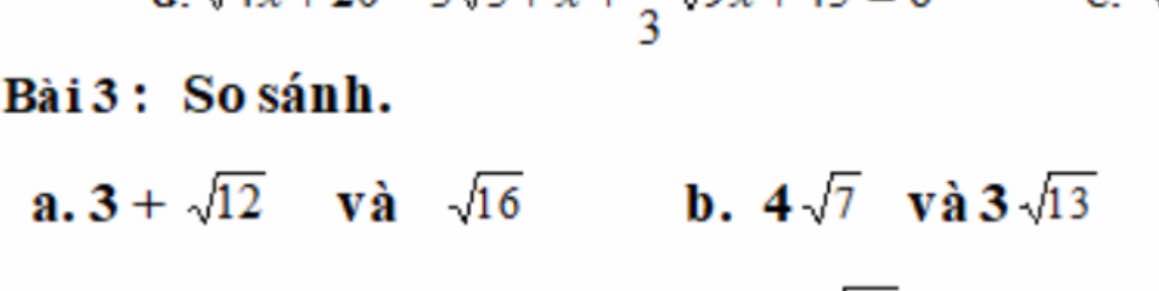
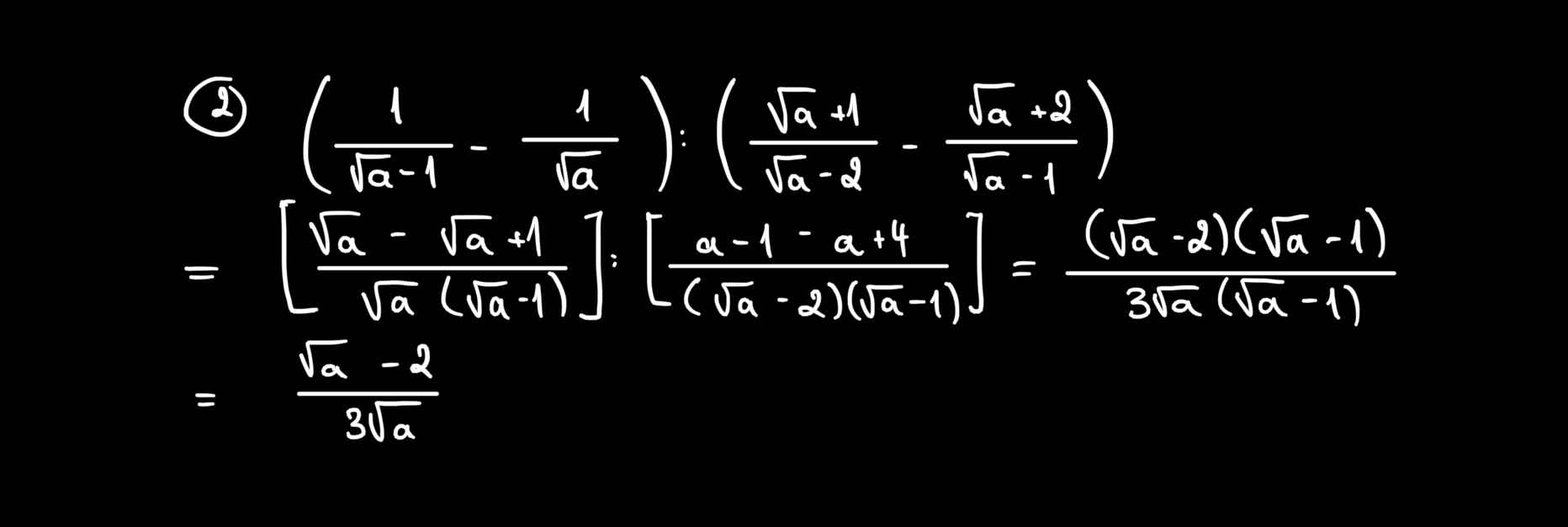
a. Giả sử: \(3+\sqrt{12}>\sqrt{16}\)
<=> \(\sqrt{12}>1\) (thỏa mãn)
Vậy \(3+\sqrt{12}>\sqrt{16}\)
b. \(4\sqrt{7}=\sqrt{4^2.7}=\sqrt{112}\)
\(3\sqrt{13}=\sqrt{3^2.13}=\sqrt{117}\)
Ta thấy: 112 < 117
Vậy \(4\sqrt{7}< 3\sqrt{13}\)
Cảm ơn bn nhiều