
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3: \(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+2\left(x>=\dfrac{1}{2}\right)\\2x-1=-x-2\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-\dfrac{1}{3}\left(nhận\right)\end{matrix}\right.\)
\(1,ĐK:x\ge1\\ PT\Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\\ 2,\Leftrightarrow2x-5=x^2-8x+16\left(x\ge4\right)\\ \Leftrightarrow x^2-10x+21=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=7\left(tm\right)\end{matrix}\right.\\ 3,\Leftrightarrow\left[{}\begin{matrix}2x-1=x+2\left(x\ge\dfrac{1}{2}\right)\\1-2x=x+2\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-\dfrac{1}{3}\left(tm\right)\end{matrix}\right.\)

a: Để phương trình có nghiệm duy nhất thì \(\left(m-3\right)\left(m+2\right)< >0\)
hay \(m\notin\left\{3;-2\right\}\)
Để phương trình vô nghiệm thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+2\right)=0\\\left(m-3\right)\left(m-1\right)< >0\end{matrix}\right.\Leftrightarrow m=-2\)
Để phương trình có vô số nghiệm thì m=3

Gọi O là trọng tâm tam giác ABC.
Dựng hình bình hành ABCE.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MO}\).
\(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{CE}+\overrightarrow{MC}=\overrightarrow{ME}\).
Từ đó \(T=3MO+3ME\ge3OE\).
Dấu bằng xảy ra khi và chỉ khi M là giao của OE và AC, tức M là trung điểm của AC.
Vậy...







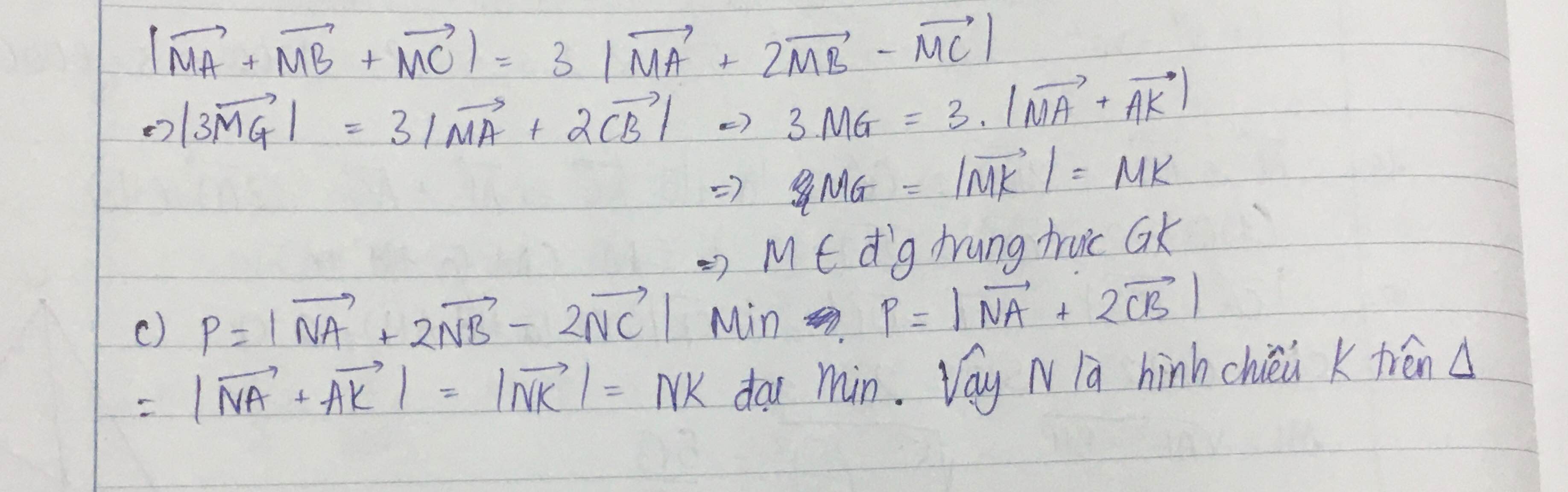 Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.
Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.


1: \(\overrightarrow{AB}=\left(-3;-1\right)\)
\(\overrightarrow{AC}=\left(1;2\right)\)