
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)
Câu 2:
\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)
\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)

Gọi O là trọng tâm tam giác ABC.
Dựng hình bình hành ABCE.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MO}\).
\(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{CE}+\overrightarrow{MC}=\overrightarrow{ME}\).
Từ đó \(T=3MO+3ME\ge3OE\).
Dấu bằng xảy ra khi và chỉ khi M là giao của OE và AC, tức M là trung điểm của AC.
Vậy...


mình nghĩ đề nó như thế này
\(\sqrt{a^2+b^2}-\sqrt{c^2+d^2}\ge\sqrt{\left(a+c\right)^2-\left(b+d^{ }\right)^2}\)
hai zế BĐT ko âm nên bình phương 2 zế ta có
\(a^2+b^2+c^2+d^2+2\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge a^2+2ac+c^2+b^2+2bd+d^2\)
\(\Leftrightarrow\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge ac+bd\left(1\right)\)
Nếu \(ac+bd< 0\)thì BĐT đc c/m
Nêu \(ac+bd\ge0\left(1\right)\Leftrightarrow\left(a^2+b^2\right)\left(c^2+d^2\right)\ge a^2c^2+b^2d^2+2acbd\)
\(\Leftrightarrow a^2c^2+a^2d^2+b^2c^2+b^2d^2\ge a^2c^2+b^2d^2+2acbd\)
\(\Leftrightarrow a^2d^2+b^2c^2-2acbd\ge0\Leftrightarrow\left(ad-bc\right)^2\ge0\)( luôn đúng )
dấu = xảy ra khi \(ad=bc\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)



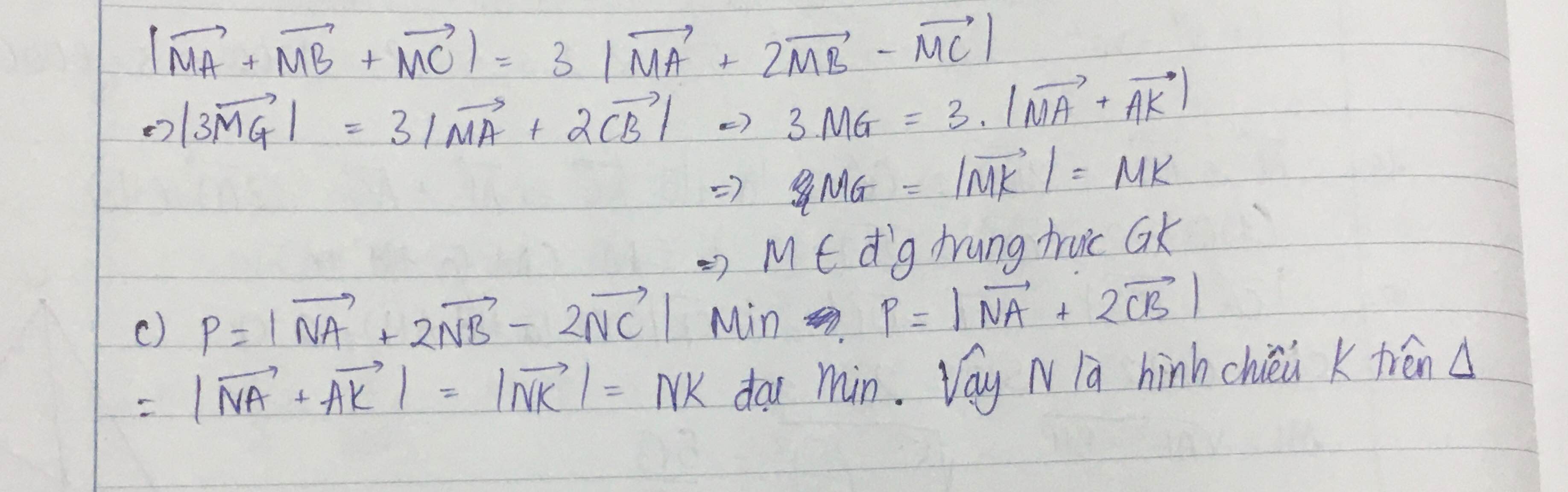 Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.
Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.

gọi thầy lâm ah
ko nhìn thấy j