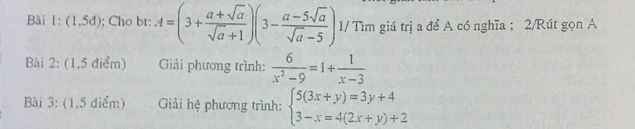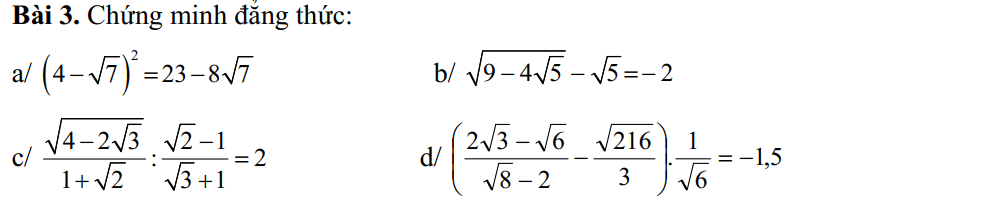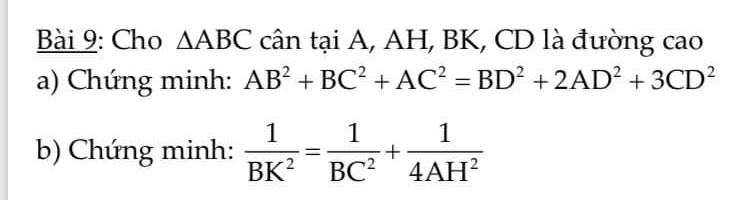K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 2 2022
Bài 2: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\Leftrightarrow\dfrac{6}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2-9+x+3}{\left(x-3\right)\left(x+3\right)}\)
Suy ra: \(x^2+x-12=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)=0\)
=>x=-4(nhận) hoặc x=3(loại)
13 tháng 2 2022
Bài 1:
a,ĐKXĐ:\(\left\{{}\begin{matrix}\sqrt{a}+1\ne0\left(luôn.đúng\right)\\\sqrt{a}-5\ne0\end{matrix}\right.\Leftrightarrow\sqrt{a}\ne5\Leftrightarrow a\ne25\)
\(b,A=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-5\sqrt{a}}{\sqrt{a}-5}\right)\)
\(\Rightarrow A=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(3-\dfrac{\sqrt{a}\left(\sqrt{a}-5\right)}{\sqrt{a}-5}\right)\)
\(\Rightarrow A=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)\)
\(\Rightarrow A=9-a\)
AT
16 tháng 7 2021
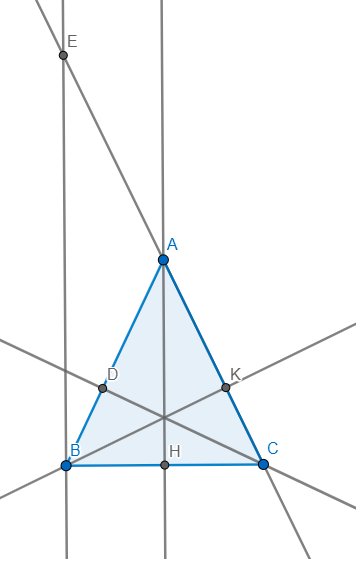
b) Từ B kẻ đường vuông góc với BC cắt AC tại E
tam giác BEC vuông tại B có \(AB=AC\Rightarrow A\) là trung điểm CE
Vì tam giác ABC cân tại A có AH là đường cao \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow AH\) là đường trung bình tam giác BEC
\(\Rightarrow AH=\dfrac{1}{2}BE\Rightarrow2AH=BE\Rightarrow4AH^2=BE^2\)
tam giác BEC vuông tại B có BK là đường cao \(\Rightarrow\dfrac{1}{BE^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
\(\Rightarrow\dfrac{1}{4AH^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
c.
\(\left\{\begin{matrix} 9x-6y=4\\ 15x-10y=7\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{6y+4}{9}\\ 15x-10y=7\end{matrix}\right.\)
\(\Rightarrow 15.\frac{6y+4}{9}-10y=7\)
\(\Leftrightarrow \frac{5}{3}(6y+4)-10y=7\Leftrightarrow \frac{20}{3}=7\) (vô lý)
Do đó hpt vô nghiệm.
d.
\(\left\{\begin{matrix} 4x+5y=3\\ x-3y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x+5y=3\\ x=3y+5\end{matrix}\right.\Rightarrow 4(3y+5)+5y=3\)
\(\Leftrightarrow 17y+20=3\Leftrightarrow 17y=-17\Leftrightarrow y=-1\)
\(x=3y+5=-3+5=2\)
Vậy HPT có nghiệm $(x,y)=(2,-1)$
Các câu còn lại bạn làm theo pp tương tự.
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
1.
HPT \(\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ 3x-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ y=3x-5\end{matrix}\right.\)
\(\Rightarrow 5x-(3x-5)=4\Leftrightarrow 2x+5=4\Leftrightarrow 2x=-1\Leftrightarrow x=\frac{-1}{2}\)
\(y=3x-5=\frac{-3}{2}-5=\frac{-13}{2}\)
Vậy HPT có nghiệm $(x,y)=(\frac{-1}{2}, \frac{-13}{2})$
8 tháng 12 2021
a, \(\dfrac{\sqrt{80}}{\sqrt{5}}\)-\(\sqrt{5}\).\(\sqrt{20}\)= \(\sqrt{16}\)-10=-6
b, (\(\sqrt{28}\)-\(\sqrt{12}\)-\(\sqrt{7}\))\(\sqrt{7}\)+2\(\sqrt{21}\)=\(\sqrt{196}\)-\(\sqrt{84}\)-7+2 \(\sqrt{21}\)=14-7=7
c, \(\sqrt[3]{2}\).\(\sqrt[3]{32}\)+\(\sqrt{2}\).\(\sqrt{32}\)=\(\sqrt[3]{64}\)+\(\sqrt{64}\)=4+8=12
d, \(2\sqrt{8\sqrt{3}}\)-\(\sqrt{2\sqrt{3}}\)-\(\sqrt{9\sqrt{12}}\)=\(4\sqrt{12}\)-\(\sqrt{12}\)-\(3\sqrt{12}\)=0
6 tháng 1 2022
b: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác AEIF có
\(\widehat{AEI}+\widehat{AFI}=180^0\)
Do đó: AEIF là tứ giác nội tiếp
