K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TL
0
5 tháng 7 2023
5:
a: Vì (d1)//(d) nên a=2
=>y=2x+b
Khi x=2 thì y=-1/2*2^2=-2
Thay x=2 và y=-2 vào (d1), ta được;
b+4=-2
=>b=-6
b: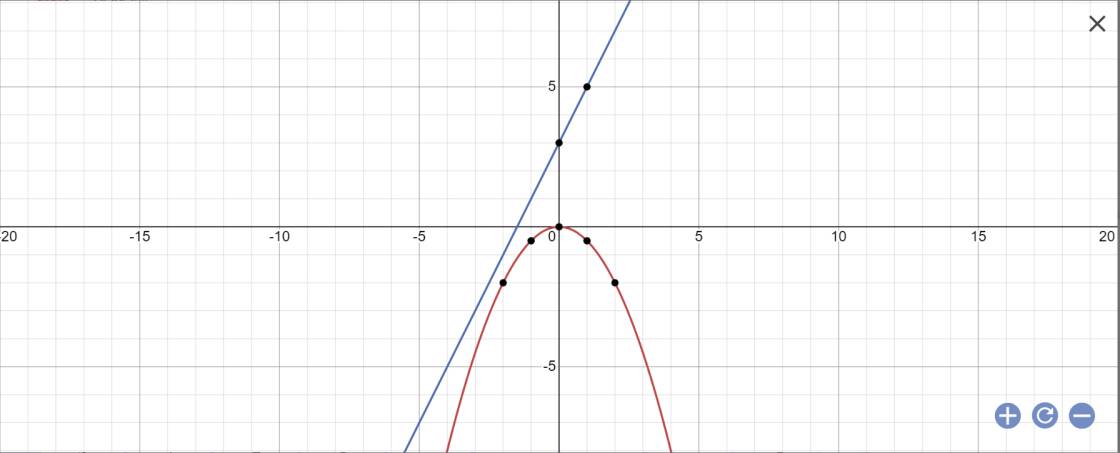 
NM
1
4 tháng 5 2019
\(\hept{\begin{cases}x^2-4x+3=0\\x^2+xy+y^2=1\end{cases}\Leftrightarrow}\hept{\begin{cases}\left(x-1\right)\left(x-3\right)=0\\x^2+xy+y^2=1\end{cases}}\)
\(\Leftrightarrow\left(I\right)\hept{\begin{cases}x=1\\x^2+xy+y^2=1\end{cases}\left(h\right)\left(II\right)\hept{\begin{cases}x=3\\x^2+xy+y^2=1\end{cases}}}\)
Giải hệ (I) \(\hept{\begin{cases}x=1\\x^2+xy+y^2=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\1+y+y^2=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y^2+y=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\y\left(y+1\right)=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\y=0\end{cases}\left(h\right)\hept{\begin{cases}x=1\\y=-1\end{cases}}}\)
Giải hệ (II)\(\hept{\begin{cases}x=3\\x^2+xy+y^2=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\9+3y+y^2=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=3\\y^2+3y+8=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\\left(y+\frac{3}{2}\right)^2+\frac{23}{4}=0\end{cases}}\)hệ vô nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
Đề bài ko chính xác, nếu x bất kì thì tồn tại vô số x để P nguyên
Nếu \(x\) nguyên thì mới có hữu hạn giá trị x
LH
4 tháng 10 2017
Bài 1: ( Tự vẽ hình )
Áp dụng tỉ số lượng giác trong tam giác vuông DEF
\(TanF=\frac{DE}{DF}=\frac{3}{5}\)
\(TanF=31\)
Bài 2: ( Tự vẽ hình, gợi ý: Vẽ tam giác vuông ABC chọn góc \(\widehat{B}\)là góc \(\alpha\))
Áp dụng định lý Pytago vào tam giác vuông ABC:
\(BC^2=AC^2+AB^2\)
\(1+cot^2\alpha=1+\frac{AB^2}{AC^2}=\frac{AC^2+AB^2}{AC^2}\)
\(1+cot^2\alpha=\frac{BC^2}{AC^2}=1:\frac{AC^2}{BC^2}\)
\(1+cot^2\alpha=1:sin^2\alpha\)
\(1+cot^2\alpha=\frac{1}{sin^2\alpha}\)
c.
\(\left\{\begin{matrix} 9x-6y=4\\ 15x-10y=7\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{6y+4}{9}\\ 15x-10y=7\end{matrix}\right.\)
\(\Rightarrow 15.\frac{6y+4}{9}-10y=7\)
\(\Leftrightarrow \frac{5}{3}(6y+4)-10y=7\Leftrightarrow \frac{20}{3}=7\) (vô lý)
Do đó hpt vô nghiệm.
d.
\(\left\{\begin{matrix} 4x+5y=3\\ x-3y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x+5y=3\\ x=3y+5\end{matrix}\right.\Rightarrow 4(3y+5)+5y=3\)
\(\Leftrightarrow 17y+20=3\Leftrightarrow 17y=-17\Leftrightarrow y=-1\)
\(x=3y+5=-3+5=2\)
Vậy HPT có nghiệm $(x,y)=(2,-1)$
Các câu còn lại bạn làm theo pp tương tự.
1.
HPT \(\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ 3x-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ y=3x-5\end{matrix}\right.\)
\(\Rightarrow 5x-(3x-5)=4\Leftrightarrow 2x+5=4\Leftrightarrow 2x=-1\Leftrightarrow x=\frac{-1}{2}\)
\(y=3x-5=\frac{-3}{2}-5=\frac{-13}{2}\)
Vậy HPT có nghiệm $(x,y)=(\frac{-1}{2}, \frac{-13}{2})$