Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
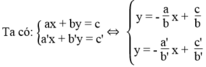
Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số góc bằng nhau và tung độ gốc khác nhau:
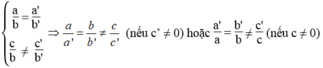
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
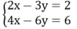
Vì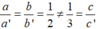 
nên hệ phương trình trên vô nghiệm
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
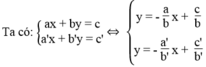
Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số góc và tung độ gốc bằng nhau:
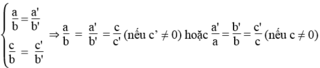
*a = 0, a’ ≠ 0
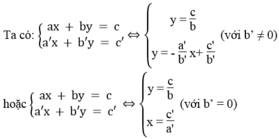
Vì hai đường thẳng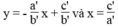 
luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*a = a’ = 0
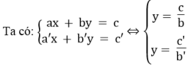
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
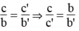
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
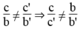
*b = 0, b’ ≠ 0
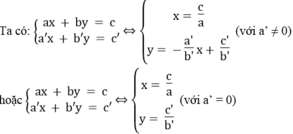
Vì hai đường thẳng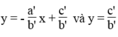 
luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*b = b’ = 0
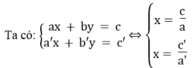
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
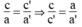
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
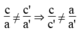
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm:
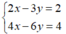
Vì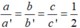 
nên hệ phương trình có vô số nghiệm
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
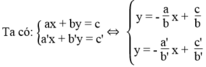
Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có hệ số góc khác nhau:
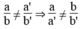
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
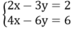
Vì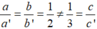 
nên hệ phương trình trên vô nghiệm
\(\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)=0\\ \Leftrightarrow x^2-ax-bx+ab+x^2-bx-cx+bc+x^2-cx-ax+ac=0\\ \Leftrightarrow3x^2-2\left(a+b+c\right)x+ab+bc+ca=0\left(1\right)\)
pt(1) là pt bậc 2 ẩn x có:
\(\Delta'=\left(-a-b-c\right)^2-3\left(ab+bc+ca\right)\\ =a^2+b^2+c^2+2ab+2bc+2ca-3\left(ab+bc+ca\right)\\ =a^2+b^2+c^2-ab-bc-ca\\ =\dfrac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\)
pt có no kép nên delta' =0
nên: \(\dfrac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\\ \Rightarrow a-b=b-c=c-a=0\\ \Rightarrow a=b=c\)
bonus: khi đó pt: \(3\left(x-a\right)^2=0\Leftrightarrow x-a=0\Leftrightarrow x=a\)
=> x=a=b=c
Đáp án B