Giups mình câu b ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 2 2022
d: \(\Leftrightarrow\dfrac{x+14}{86}+1+\dfrac{x+15}{85}+1+\dfrac{x+16}{84}+1+\dfrac{x+17}{83}+1+\dfrac{x+116}{4}-4=0\)
=>x+100=0
hay x=-100
a: \(\Leftrightarrow2\left(x+1\right)^2+3\left(x^2-3x+2\right)=\left(3x-1\right)\left(x-4\right)+56\)
\(\Leftrightarrow2x^2+4x+2+3x^2-9x+6-\left(3x^2-13x+4\right)-56=0\)
\(\Leftrightarrow5x^2-5x-48-3x^2+13x-4=0\)
\(\Leftrightarrow2x^2+8x-52=0\)
\(\Leftrightarrow x^2+4x-13=0\)
\(\Leftrightarrow\left(x+2\right)^2=17\)
hay \(x\in\left\{-\sqrt{17}-2;\sqrt{17}-2\right\}\)
15 tháng 6 2023
c: Xét ΔBKC có
BH,CA là đường cao
BH cắt CA tại I
=>I là trực tâm
=>KI vuông góc BC tại D
góc DAC=góc DAI=góc HBC
góc HAC=góc DKC
mà góc HBC=góc DKC
nên góc DAC=góc HAC
=>AC là phân giác của góc DAH
12 tháng 1 2020
\(2.a^2+2.b^2+2c^2-2ab-2bc-2ac=4a^2+4b^2+4c^2-4ab-4bc-4ac\)
\(2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2=0\right)\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}\Rightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Rightarrow}a=b=c\left(dpcm\right)}\)
VD
11 tháng 3 2022
Tổng thời gian đi và về là: 9h30'-7h-15 phút = 2h15' = 9/4h
Gọi quãng đường AB là x(x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{50}\left(h\right)\)
Thời gian đi từ A đến B là \(\dfrac{x}{40}\left(h\right)\)
Theo bài ra ta có pt:
\(\dfrac{x}{50}+\dfrac{x}{40}=\dfrac{9}{4}\\ \Leftrightarrow\dfrac{4x}{200}+\dfrac{5x}{200}=\dfrac{450}{200}\\ \Leftrightarrow9x=450\\ \Leftrightarrow x=50\left(tm\right)\)
Vậy quãng đường AB là 50 km
31 tháng 1 2023
a: Xét ΔABK có DH//BK
nên DH/BK=AD/AB=2/3
b: DH/BK=2/3
=>DH=2/3BK
mà DH+BK=20
nên DH=8cm; BK=12cm
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
NP
2
28 tháng 1 2023
a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)
L
23 tháng 5 2021
a) \(M=\dfrac{x}{x-2}:\left(\dfrac{2x}{x^2-2x}-\dfrac{3}{x}\right)\)
\(M=\dfrac{x}{x-2}:\left(\dfrac{2x}{x\left(x-2\right)}-\dfrac{3\left(x-2\right)}{x\left(x-2\right)}\right)\)
\(M=\dfrac{x}{x-2}:\left(\dfrac{2x-3x+6}{x\left(x-2\right)}\right)\)
\(M=\dfrac{x}{x-2}.\dfrac{x\left(x-2\right)}{6-x}\)
\(M=\dfrac{x^2}{6-x}\)
b) \(x^2-3x=0\)
\(x\left(x-3\right)=0\)
x=0 (KTMĐK) hoặc x=3 (TMĐK)
Thay x=3 vào M ta có :
\(M=\dfrac{3^2}{6-3}=\dfrac{9}{3}=3\)
c) \(M\ge0\rightarrow\dfrac{x^2}{6-x}\ge0\)
\(x^2\ge0\rightarrow6-x\ge0\)
\(x\le6\)
Kết hợp với ĐK, ta có : \(x\le6,x\ne0,x\ne2\)
15 tháng 8 2021
a: Ta có: \(A=\left(1-2x\right)\left(1+2x\right)+\left(2x-1\right)\left(2x-3\right)\)
\(=1-4x^2+4x^2-6x-2x+3\)
\(=-8x+4\)
\(=-8\cdot\left(-1\right)+4=12\)
b: Ta có: \(B=\left(1-x\right)\left(1+x\right)+\left(x-1\right)\left(x+3\right)\)
\(=1-x^2+x^2+3x-x-3\)
\(=2x-2\)
=0
c: Ta có: \(C=\left(1-y\right)\left(y+2\right)-\left(2-y\right)\left(3+y\right)\)
\(=y+2-y^2-2y+\left(y-2\right)\left(y+3\right)\)
\(=-y^2-y+2+y^2+3y-2y-6\)
\(=-4\)
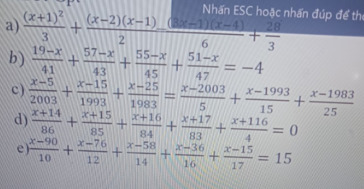
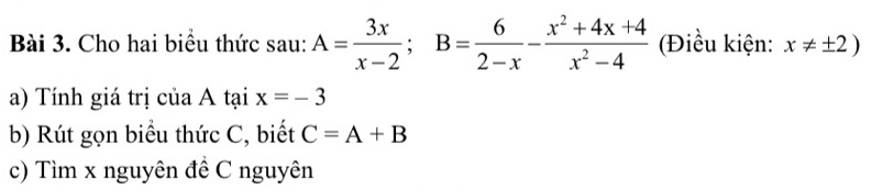
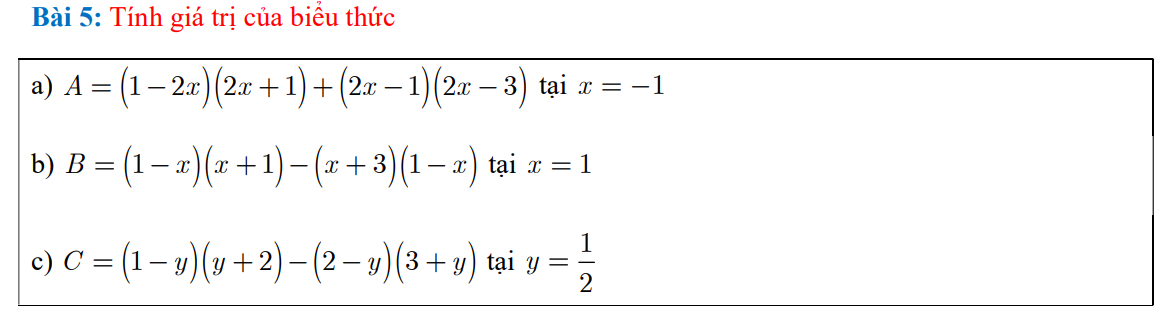
b: AF*AB=AE*AC
=>AF/AC=AE/AB
mà góc A chung
nên ΔAFE đồng dạng với ΔACB
=>góc AFE=góc ACB