
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a)\)
\(A=\left(m-1\right)^3-\left(m-2\right)^3\)
\(=\left(m^3-3m^2+3m-1\right)-\left(m^3-6m^2+12m-8\right)\)
\(=m^3-3m^2+3m-1-m^3+6m^2-12m+8\)
\(=3m^2-9m+7\)
\(B=\left(3m-1\right)\left(3m+1\right)\)
\(=9m^2-1\)
\(\dfrac{1}{9}A=B-7\)
\(\Rightarrow\dfrac{1}{9}\left(3m^2-9m+7\right)=9m^2-1-7\)
\(\Rightarrow3m^2-9m+7=81m^2-72\)
\(\Rightarrow78m^2+9m-79=0\)
\(\Rightarrow m=\dfrac{-9\pm\sqrt{24729}}{156}\)
\(b)\)
\(A< B\)
\(\Rightarrow3m^2-9m+7< 9m^2-1\)
\(\Rightarrow6m^2+9m-8>0\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{-9+\sqrt{273}}{12}\\m< \dfrac{-9-\sqrt{273}}{12}\end{matrix}\right.\)


bn bị mất gốc như vậy sẽ khó mà có thể thi lên lớp 10 đc
Có thể sẽ đc, nếu bn chăm chỉ hok thêm ở các trung tâm dạy toán
Đổi lại nó cũng sẽ mất rất nhiều thời gian nên bn cũng cần phải kiên nhẫn
=> Đó lak ý kiến riêng của mk, tùy bạn lựa chọn.




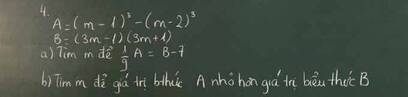



a)a)
EE đối xứng với DD qua OO
⇒O⇒O là trung điểm của DEDE
Xét tứ giác ADCEADCE có:
Hai đường chéo DEDE và ACAC cắt nhau tại trung điểm OO của mỗi đường
⇒⇒ Tứ giác ADCEADCE là hình bình hành
Mà ˆADC=90o(AD⊥DC)ADC^=90o(AD⊥DC)
⇒⇒ Hình bình hành ADCEADCE là hình chữ nhật
b)b)
Xét ΔADCΔADC có:
II là trung điểm của ADAD
OO là trung điểm của ACAC
⇒IO⇒IO là đường trung bình của ΔADCΔADC
⇒IO//BD⇒IO//BD
Trong ΔBDEΔBDE có:
OO là trung điểm của DEDE
IO//BDIO//BD
⇒I⇒I là trung điểm của BEBE
c)c)
ΔABCΔABC cân có ADAD đường cao
⇒AD⇒AD đồng thời là đường trung tuyến
⇒D⇒D là trung điểm của BCBC
⇒BD=BC2=122=6(cm)⇒BD=BC2=122=6(cm)
ΔABDΔABD vuông tại DD nên theo pi-ta-go
AB2=BD2+AD2AB2=BD2+AD2
⇒AD=√AB2−BD2=√102−62=8(cm)⇒AD=AB2-BD2=102-62=8(cm)
Gọi TT là trung điểm của ECEC
Trong ΔBECΔBEC có:
TT là trung điểm của ECEC
II là trung điểm của BEBE
⇒IT⇒IT là đường trung bình của ΔBECΔBEC
⇒IT//BD⇒IT//BD mà IO//BDIO//BD
⇒I;O;T⇒I;O;T thẳng hàng
Từ IT//BDIT//BD hay IT//DCIT//DC
Xét tứ giác IDCTIDCT có:
ID//TC(cmt);IT//CD(cmt)ID//TC(cmt);IT//CD(cmt)
⇒⇒ Tứ giác IDCTIDCT là hình bình hành
⇒IT=DC=6cm(DC=BC2=6cm)⇒IT=DC=6cm(DC=BC2=6cm)
AEDCAEDC là hình chữ nhật
⇒AC=DE⇒AC=DE
⇒AC2=DE2⇒AC2=DE2
⇒OD=OC⇒OD=OC
IDCTIDCT là hình bình hành có ˆIDC=90oIDC^=90o
⇒IDCT⇒IDCT là hình chữ nhật
Xét ΔIODΔIOD và ΔTOCΔTOC có:
ID=TC(IDCTID=TC(IDCT là hình chữ nhật)
OA=OC(cmt)OA=OC(cmt)
ˆOID=ˆOTC=90oOID^=OTC^=90o
⇒ΔIOD=ΔTOC(cạnh huyền-cạnh góc vuông)⇒ΔIOD=ΔTOC(cạnh huyền-cạnh góc vuông)
⇒IO=TO⇒IO=TO
⇒O⇒O là trung điểm của ITIT
⇒OI=IT2=62=3(cm)⇒OI=IT2=62=3(cm)
⇒SΔADO=12.AD.OI=12.8.3=12(cm2)⇒SΔADO=12.AD.OI=12.8.3=12(cm2)
d)d)
AE//DCAE//DC hay AE//BDAE//BD
AE=DC(ADCEAE=DC(ADCE là hình chữ nhật)
Mà BD=DC(DBD=DC(D là trung điểm của BCBC)
⇒AE=BD⇒AE=BD
Xét tứ giác AEDBAEDB có:
AE//DB(cmt);AE=BD(cmt)AE//DB(cmt);AE=BD(cmt)
⇒⇒ Tứ giác AEDBAEDB là hình bình hành
⇒AK//DE⇒AK//DE
⇒⇒ Tứ giác AKDEAKDE là hình thang
Giả sử ΔABCΔABC là tam giác đều
IO//BDIO//BD hay IK//BDIK//BD
Trong ΔABDΔABD có:
II là trung điểm của ADAD
IK//BDIK//BD
⇒K⇒K là trung điểm của ABAB
Trong tam giác ABCABC có KDKD là đường trung bình
⇒KD=12AC=12AB=12BC⇒KD=12AC=12AB=12BC
⇒KD=KB=BD⇒KD=KB=BD
⇒ΔKBD⇒ΔKBD đều
Trong ΔABCΔABC có ODOD là đường trung bình
⇒OD=12AB=12BC=12AC⇒OD=12AB=12BC=12AC
⇒OD=DC=OC⇒OD=DC=OC
⇒ΔODC⇒ΔODC đều
⇒ˆKDE=180o−60o−60o=60o⇒KDE^=180o-60o-60o=60o
ΔDCEΔDCE vuông tại CC
⇒ˆDEC=180o−90o−60o=30o⇒DEC^=180o-90o-60o=30o
Lại có:
ˆDEC+ˆAED=90oDEC^+AED^=90o
⇒ˆAED=90o−30o=60o⇒AED^=90o-30o=60o
⇒ˆAED=ˆKDE=60o⇒AED^=KDE^=60o
⇒⇒ hình thang AKDEAKDE là hình thang cân
Vậy tam giác ABCABC đều thì tứ giác AKDEAKDE là hình thang cân
Bài 5.5.
P=2bc−20163c−2bc+2016−2b3−2b+ab+4032−3ac3ac−4032+2016aP=2bc-20163c-2bc+2016-2b3-2b+ab+4032-3ac3ac-4032+2016a
P=2bc−abc3c−2bc+abc−2b3−2b+ab+2abc−3ac3ac−2abc+abc.aP=2bc-abc3c-2bc+abc-2b3-2b+ab+2abc-3ac3ac-2abc+abc.a
P=2bc−abc3c−2bc+abc−2bc3c−2bc+abc+2bc−3c3c−2bc+abcP=2bc-abc3c-2bc+abc-2bc3c-2bc+abc+2bc-3c3c-2bc+abc
P=2bc−abc−2bc+2bc−3c3c−2bc+abcP=2bc-abc-2bc+2bc-3c3c-2bc+abc
P=2bc−abc−3c3c−2bc+abcP=2bc-abc-3c3c-2bc+abc
P=−(3c−2bc+abc)3c−2bc+abcP=-(3c-2bc+abc)3c-2bc+abc
P=−1P=-1
Vậy P=−1