K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 3 2016
d) Điều kiện x>0. Áp dụng công thức đổi cơ số, ta có :
\(\log_2x+\log_3x+\log_4x=\log_{20}x\)
\(\Leftrightarrow\log_2x+\frac{\log_2x}{\log_23}+\frac{\log_2x}{\log_24}=\frac{\log_2x}{\log_220}\)
\(\Leftrightarrow\log_2x\left(1+\frac{1}{\log_23}+\frac{1}{2}+\frac{1}{\log_220}\right)=0\)
\(\Leftrightarrow\log_2x\left(\frac{3}{2}+\log_22-\log_{20}2\right)=0\)
Ta có \(\frac{3}{2}+\log_22-\log_{20}2>\frac{3}{2}+0-1>0\)
Do đó, từ phương trình trên, ta phải có \(\log_2x=0\) hay \(x=2^0=1\)
Vậy nghiệm duy nhất của phương trình là \(x=1\)
28 tháng 3 2016
c) Điều kiện x>0, đưa về cùng cơ số 5, ta có :
\(\log_5x^3+3\log_{25}x+\log_{\sqrt{25}}\sqrt{x^3}=\frac{11}{2}\)
\(\Leftrightarrow3\log_5x+3\log_{5^2}x+\log_{5^{\frac{3}{2}}}x^{\frac{3}{2}}=\frac{11}{2}\)
\(\Leftrightarrow3\log_5x+3\frac{1}{2}\log_5x+\frac{3}{2}.\frac{2}{3}\log_5x=\frac{11}{2}\)
\(\Leftrightarrow\frac{11}{2}\log_5x=\frac{11}{2}\)
\(\Leftrightarrow\log_5x=1\)
\(\Leftrightarrow x=5^1=5\) thỏa mãn
Vậy phương trình chỉ có 1 nghiệ duy nhất \(x=5\)
HP
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
\(\Leftrightarrow3^{x^2}.4^{x+1}=3^{-x}\)
Lấy logarit cơ số 3 hai vế:
\(\Rightarrow log_3\left(3^{x^2}.4^{x+1}\right)=log_3\left(3^{-x}\right)\)
\(\Leftrightarrow x^2+\left(x+1\right)log_34=-x\)
\(\Leftrightarrow x^2+x+\left(x+1\right)log_34=0\)
\(\Leftrightarrow x\left(x+1\right)+\left(x+1\right)log_34=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+log_34\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-log_34=-2log_32\end{matrix}\right.\)
BT
1 tháng 12 2017
\(log_2\left(5^{x+1}-25^x\right)=2\) \(\Leftrightarrow5^{x+1}-25^x=2^2\)\(\Leftrightarrow-\left(5^x\right)^2+5.5^x-4=0\).
Đặt \(5^x=t\left(t>0\right)\), phuyowng trình trở thành:
\(-t^2+5t-4=0\) \(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\).
\(t=1\Leftrightarrow5^x=1\) \(\Leftrightarrow x=0\).
\(t=4\Leftrightarrow5^x=4\Leftrightarrow x=log_54\).
PT
1
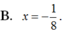
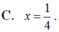
Đáp án C