

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Toàn bộ nghiệm của 3 pt này đều là nghiệm thực, không có nghiệm phức nào
a. \(x^2-3x-2=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{17}}{2}\\x=\dfrac{3-\sqrt{17}}{2}\end{matrix}\right.\)
b. \(x^4-5x^2+6=0\Rightarrow\left[{}\begin{matrix}x^2=2\\x^2=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\pm\sqrt{2}\\x=\pm\sqrt{3}\end{matrix}\right.\)
c. \(-x^2+4x+5=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=5\end{matrix}\right.\)


a) Bất phương trình đã cho tương đương với hệ sau:
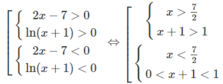
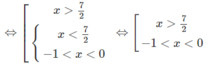
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
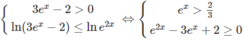
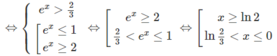
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )

-log22 x2_ log2x2- 20=0
↔ pt này vô ng bạn ơi!!! xem lại đầu bài.
Bài này phương trình có tận 4 nghiệm chứ không phải vô nghiệm đâu bạn Đỗ đại học nhé
Điều kiện \(x\ne0\)
Ta có từ phương trình ban đầu cho \(\Leftrightarrow4\log_2^2\left|x\right|-2\log_2\left|x\right|-20=0\)
\(\Leftrightarrow2\log_2^2\left|x\right|-\log_2\left|x\right|-10=0\)
Đặt \(t=\log_2\left|x\right|\) ta được phương trình \(2t^2-t-10=0\Leftrightarrow\begin{cases}t=-2\\t=\frac{5}{2}\end{cases}\)
Với \(t=2\Rightarrow\log_2\left|x\right|=-2\Leftrightarrow\left|x\right|=\frac{1}{4}\Leftrightarrow x=\pm\frac{1}{4}\)
Với \(t=\frac{5}{2}\Rightarrow\log_2\left|x\right|=\frac{5}{2}\Leftrightarrow\left|x\right|=\sqrt{32}\Leftrightarrow x=\pm\sqrt{32}\)
Vậy phương trình có 4 nghiệm : \(x=\frac{1}{4};x=-\frac{1}{4};x=\sqrt{32};x=-\sqrt{32}\)