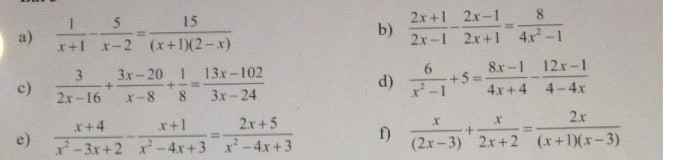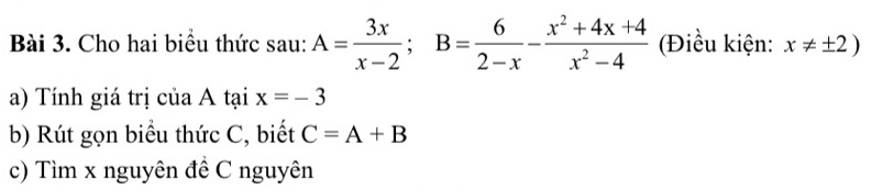giải giúp mình câu b, c với ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giải giúp mình câu c với ạ, mình cảm ơnnnnn
LD
3 tháng 4 2022
Nếu là câu c
c, Ta có : BD là phân giác \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(1\right)\)
Ta có : BK là phân giác \(\widehat{ABH}\)
\(\Rightarrow\dfrac{HK}{AK}=\dfrac{BH}{AB}\left(2\right)\)
Ta có: ΔHBA ~ ΔABC (cmt )
(*nếu chưa c/m tam giác đồng dạng thì hãy c/m, làm r thì khỏi )
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{AB}{AC}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\dfrac{AD}{DC}=\dfrac{HK}{AK}\)
\(\Rightarrow AK.AD=HK.CD\left(đpcm\right)\)
13 tháng 1 2023
c: (x-2)^2+2(2-x)=0
=>(x-2)^2-2(x-2)=0
=>(x-2)(x-4)=0
=>x=2 hoặc x=4
25 tháng 6 2023
c: ĐKXĐ: x<>8
\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)
=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)
=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)
=>8(8x-93)=6x-48
=>64x-744-6x+48=0
=>58x=696
=>x=12
d: ĐKXĐ: x<>1; x<>-1
\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)
=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20
=>20x^2+2x=20x^2+4
=>2x=4
=>x=2(loại)
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
TD
4
NP
2
28 tháng 1 2023
a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)
