
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(2\sqrt{3}-\sqrt{4+x^2}=0\Leftrightarrow\sqrt{4+x^2}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\Leftrightarrow x^2=8\Leftrightarrow x=\pm2\sqrt{2}\)
b, \(\sqrt{16x+16}-\sqrt{9x+9}=0\)ĐK : x >= -1
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=0\Leftrightarrow\sqrt{x+1}=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
c, \(\sqrt{4\left(x+2\right)^2}=8\Leftrightarrow2\left|x+2\right|=8\Leftrightarrow\left|x+2\right|=4\)
TH1 : \(x+2=4\Leftrightarrow x=2\)
TH2 : \(x+2=-4\Leftrightarrow x=-6\)
c: Ta có: \(\sqrt{4\left(x+2\right)^2}=8\)
\(\Leftrightarrow\left|x+2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)


1. ĐKXĐ: $x\geq 1$
PT $\Leftrightarrow \sqrt{x-1}=13-x$
\(\Rightarrow \left\{\begin{matrix} 13-x\geq 0\\ x-1=(13-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 13\\ x^2-27x+170=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 13\\ (x-17)(x-10)=0\end{matrix}\right.\)
\(\Rightarrow x=10\) (tm)
2. ĐKXĐ: $x\geq 3$
\(3\sqrt{x+34}-3\sqrt{x-3}=1\)
\(\Leftrightarrow 3\sqrt{x+34}=3\sqrt{x-3}+1\)
\(\Rightarrow 9(x+34)=9x+6\sqrt{x-3}-26\)
\(\Leftrightarrow \frac{166}{3}=\sqrt{x-3}\)
$\Leftrightarrow x-3=\frac{27556}{9}$
$\Leftrightarrow x=\frac{27583}{9}$ (tm)


\(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\\ =\dfrac{2-\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\dfrac{2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\\ =\dfrac{2-\sqrt{3}+2+\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}\\ =\dfrac{2+2}{4-3}\\ =4\)
Ta có: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=2-\sqrt{3}+2+\sqrt{3}\)
=4

Bài 5:
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)
b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)
c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)
Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)

1: \(\dfrac{x^2-5}{x-\sqrt{5}}=x+\sqrt{5}\)
2: \(\dfrac{1-b\sqrt{b}}{1-\sqrt{b}}=1+\sqrt{b}+b\)
3: \(\dfrac{1-\sqrt{8}}{1+\sqrt{2}}=-5+3\sqrt{2}\)

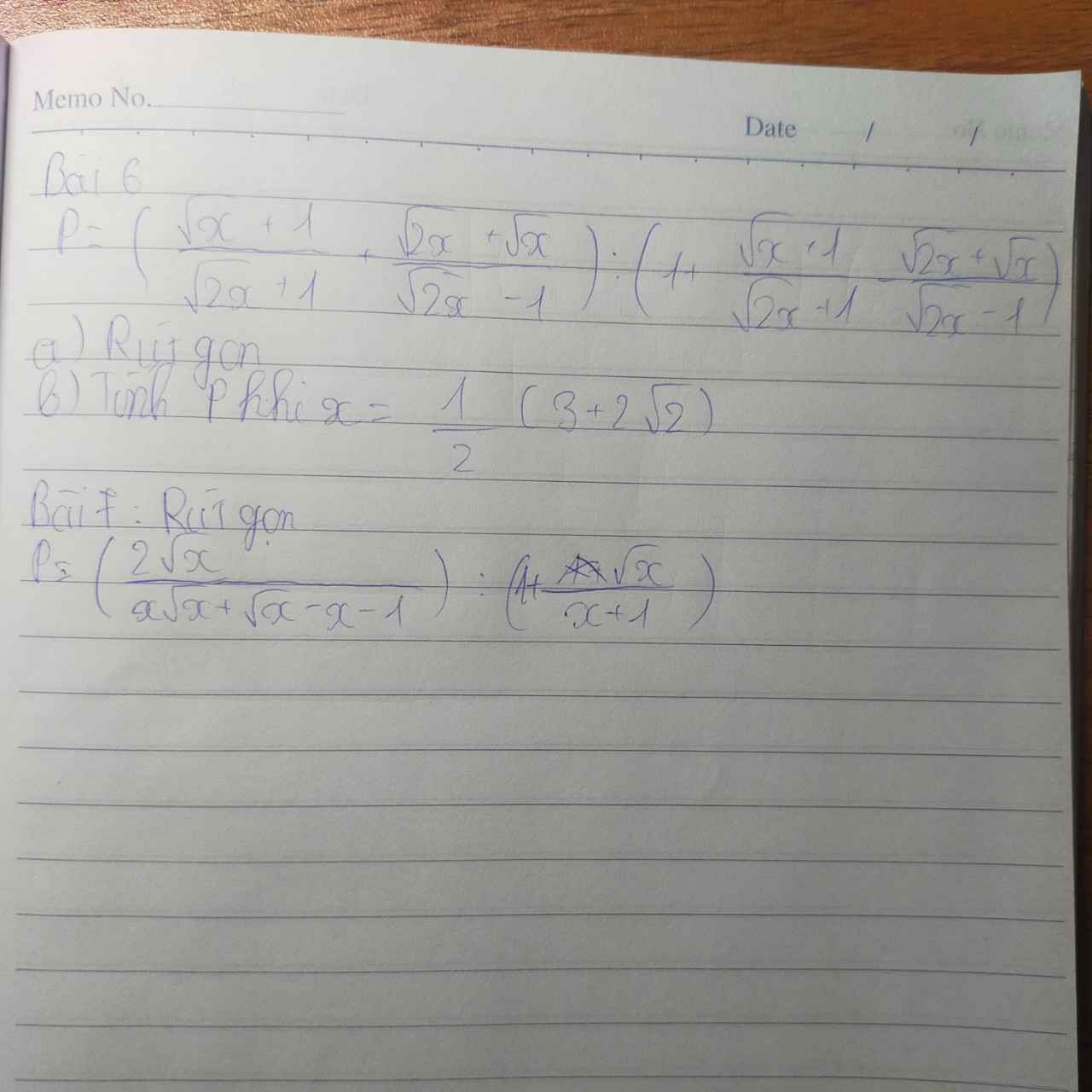
 Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.







Bài 7:
Ta có: \(P=\left(\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right):\left(1+\dfrac{\sqrt{x}}{x+1}\right)\)
\(=\dfrac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{x+1}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}}{x\sqrt{x}-1}\)