
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)


b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)

2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40

Bài 5:
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)
b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)
c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)
Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)

Ptr có `2` nghiệm phân biệt `<=>\Delta' > 0`
`=>(m+1)^2-m^2+2m-3 > 0`
`<=>m^2+2m+1-m^2+2m-3 > 0`
`<=>m > 1/2`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=2m+2),(x_1.x_2=c/a=m^2-2m+3):}`
Ta có: `1/[x_1 ^2]-[4x_2]/[x_1]+3x_2 ^2=0`
`=>1-4x_1.x_2+3(x_1.x_2)^2=0`
`<=>1-4(m^2-2m+3)+3(m^2-2m+3)^2=0`
`<=>[(m^2-2m+3=1),(m^2-2m+3=1/3):}`
`<=>[(m^2-2m+2=0(VN)),(m^2-2m+8/3=0(VN)):}`
`=>` Không có `m` thỏa mãn.





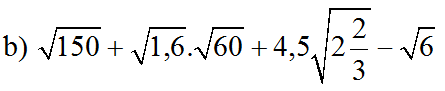




\(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\\ =\dfrac{2-\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\dfrac{2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\\ =\dfrac{2-\sqrt{3}+2+\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}\\ =\dfrac{2+2}{4-3}\\ =4\)
Ta có: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=2-\sqrt{3}+2+\sqrt{3}\)
=4