K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BD
1
22 tháng 7 2021
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
NH
1
9 tháng 10 2021
Bài 7:
Ta có: \(P=\left(\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right):\left(1+\dfrac{\sqrt{x}}{x+1}\right)\)
\(=\dfrac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{x+1}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}}{x\sqrt{x}-1}\)
NT
1
28 tháng 10 2021
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật
14 tháng 10 2021
Bài 1:
b: Xét ΔADC vuông tại D có DH là đường cao ứng với cạnh huyền AC
nên \(\left\{{}\begin{matrix}AD^2=AH\cdot AC\\DC^2=CH\cdot CA\end{matrix}\right.\)
\(\Leftrightarrow\left(\dfrac{BC}{DC}\right)^2=\dfrac{AH}{CH}\)
29 tháng 6 2021
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2) Thay \(x=4-2\sqrt{3}\) vào P, ta được:
\(P=\dfrac{2\left(\sqrt{3}-1\right)+1}{\sqrt{3}-1+1}=\dfrac{2\sqrt{3}-2+1}{\sqrt{3}}=\dfrac{2\sqrt{3}-1}{\sqrt{3}}=\dfrac{6-\sqrt{3}}{3}\)
LB
1
9 tháng 10 2021
b: Xét ΔABH vuông tại H có
\(AB^2=AH^2+HB^2\)
hay AH=12(cm)
Xét ΔAHB vuông tại H có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{5}{13}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{12}{5}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{5}{12}\)
1 tháng 7 2023
\(Q=x-2-2\sqrt{x-2}+4\)
\(=\left(\sqrt{x-2}-1\right)^2+3>=3\)
Dấu = xảy ra khi x=3
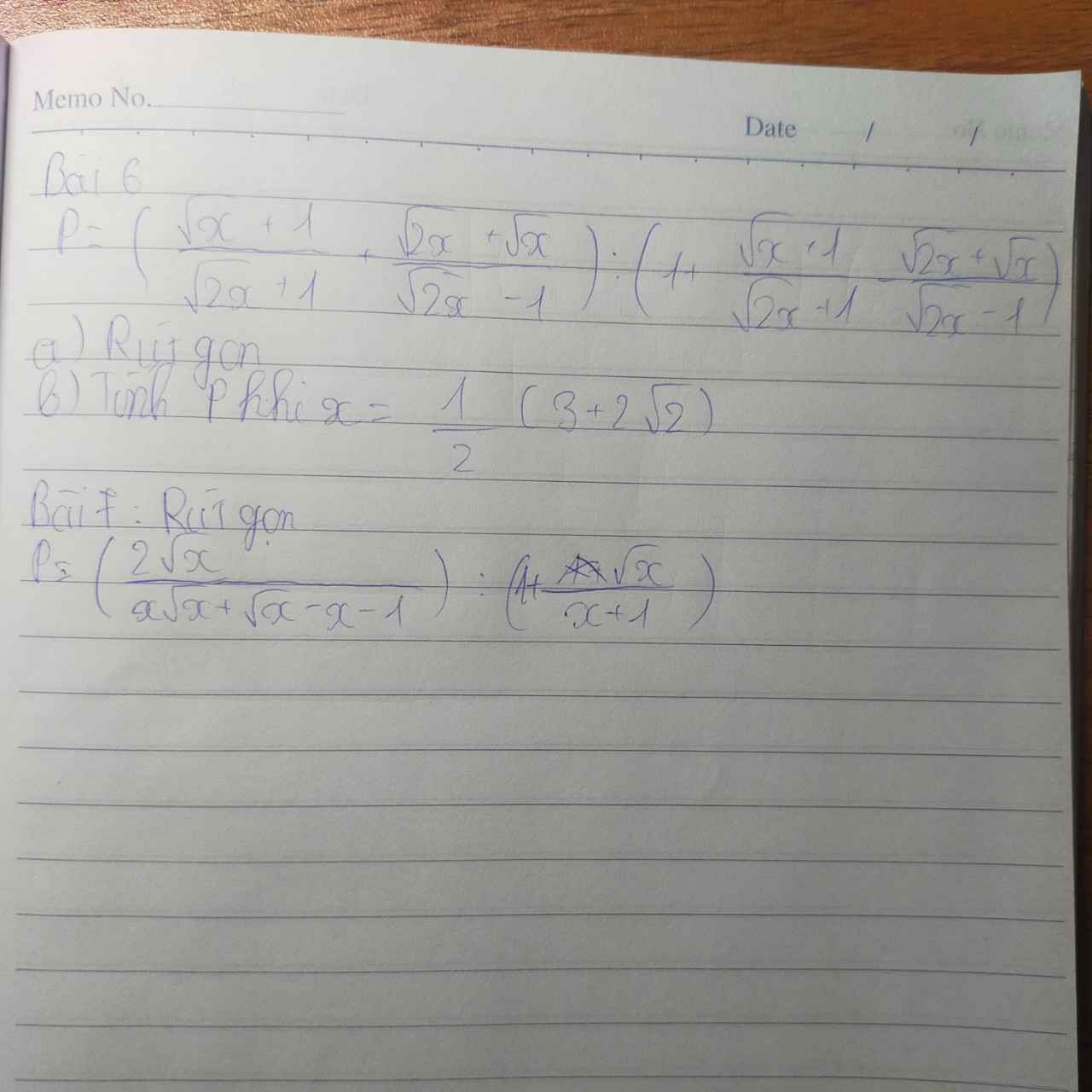
1. ĐKXĐ: $x\geq 1$
PT $\Leftrightarrow \sqrt{x-1}=13-x$
\(\Rightarrow \left\{\begin{matrix} 13-x\geq 0\\ x-1=(13-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 13\\ x^2-27x+170=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 13\\ (x-17)(x-10)=0\end{matrix}\right.\)
\(\Rightarrow x=10\) (tm)
2. ĐKXĐ: $x\geq 3$
\(3\sqrt{x+34}-3\sqrt{x-3}=1\)
\(\Leftrightarrow 3\sqrt{x+34}=3\sqrt{x-3}+1\)
\(\Rightarrow 9(x+34)=9x+6\sqrt{x-3}-26\)
\(\Leftrightarrow \frac{166}{3}=\sqrt{x-3}\)
$\Leftrightarrow x-3=\frac{27556}{9}$
$\Leftrightarrow x=\frac{27583}{9}$ (tm)