T
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NC
31 tháng 8 2020
Bài làm:
Vì a,b,c khác 0 nên:
Ta có: \(a\left(y+z\right)=b\left(z+x\right)=c\left(x+y\right)\)
\(\Leftrightarrow\frac{y+z}{bc}=\frac{z+x}{ca}=\frac{x+y}{ab}\) (1) (chia cả 3 vế cho abc)
Áp dụng t/c dãy tỉ số bằng nhau ta được:
\(\left(1\right)=\frac{x+y-z-x}{ab-ca}=\frac{y+z-x-y}{bc-ab}=\frac{z+x-y-z}{ca-bc}\)
\(=\frac{y-z}{a\left(b-c\right)}=\frac{z-x}{b\left(c-a\right)}=\frac{x-y}{c\left(a-b\right)}\)
=> đpcm
26 tháng 12 2016
a) xem lại thiếu cái đk gì đó
b) thích chọn số nào tùy
\(\frac{1}{2}=\frac{2}{4}< \frac{3}{4}< \frac{4}{4}< \frac{5}{4}< \frac{6}{4}< \frac{7}{4}< \frac{8}{4}< \frac{9}{4}< \frac{10}{4}=\frac{5}{2}\)
KB
2
KN
26 tháng 7 2019
Đặt \(\frac{x}{z}=\frac{z}{y}=k\Rightarrow\hept{\begin{cases}x=zk\\z=yk\end{cases}}\)(1)
\(\Rightarrow\frac{x^2+z^2}{y^2+z^2}=\frac{\left(zk\right)^2+\left(yk\right)^2}{y^2+z^2}=\frac{k^2\left(z^2+y^2\right)}{y^2+z^2}=k^2\)(2)
Từ (1) suy ra \(x=yk^2\Rightarrow\frac{x}{y}=\frac{yk^2}{y}=k^2\)(3)
Từ (2) và (3) suy ra \(\frac{x^2+z^2}{y^2+z^2}=\frac{x}{y}\)
26 tháng 7 2019
Đặt\(\frac{x}{z}\)=\(\frac{z}{y}\)= k
=> x = k . z ; z = k . y
=>\(\frac{x^2+y^2}{y^2+z^2}\)= \(\frac{\left(k.z\right)^2+\left(k.y\right)^2}{y^2+z^2}\)=\(\frac{k^2.\left(z^2+y^2\right)}{z^2+y^2}\)= \(k^2\)(1)
=> \(\frac{x}{y}\)= \(\frac{k.z}{y}\)=\(\frac{k.k.y}{y}\)=\(\frac{k^2.y}{y}\)= \(k^2\)(2)
Từ (1);(2)
=> ĐPCM
~~~~~Chúc bạn hok tốt~~~~~
19 tháng 8 2015
\(x=\frac{a}{m}=\frac{2a}{2m}=\frac{a+a}{2m}\)
mà x<y=>a<b=> \(\frac{a+a}{2m}
L
1
TN
1 tháng 12 2016
\(\frac{2.\left(x+y\right)}{30}=\frac{5.\left(y+z\right)}{30}=\frac{3\left(x+z\right)}{30}\)
= \(\frac{x+y}{15}=\frac{y+z}{6}=\frac{x+z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x+y}{15}=\frac{y+z}{6}=\frac{x+z}{10}\)=\(\frac{x+z-y-z}{10-6}=\frac{x-y}{4}\)
\(\frac{x+y}{15}=\frac{y+z}{6}=\frac{x+z}{10}\)=\(\frac{x+y-x-z}{15-10}=\frac{y-z}{5}\)
---> dp cm
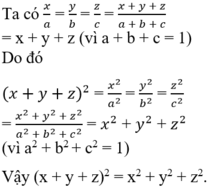
Áp dụng bất đẳng thức Cauchy - Schwarz dưới dạng Engel ta có :
\(x^2+y^2+z^2\ge\frac{\left(x+y+z\right)^2}{1+1+1}=\frac{1}{3}\left(x+y+z=1\right)\)
Dấu ''='' xảy ra <=> x = y = z = \(\frac{1}{3}\)
Vậy x2 + y2 + z2 \(\ge\frac{1}{3}\) tại x = y = z = \(\frac{1}{3}\)