
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

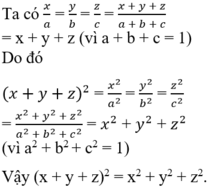

\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) ⇒ \(\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{a^2}\) = \(\dfrac{y^2}{b^2}\) = \(\dfrac{z^2}{c^2}\) = \(\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\) = \(\dfrac{x^2+y^2+z^2}{1}\) = \(x^2+y^2+z^2\) (1)
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}\) = \(\dfrac{x+y+z}{1}\) = \(x+y+z\)
\(\dfrac{x}{a}\) = \(x+y+z\) ⇒ \(\dfrac{x^2}{a^2}\) = (\(x+y+z\))2 (2)
Từ (1) và (2) ta có :
\(\dfrac{x^2}{a^2}\) = \(x^2\) + y2 + z2 = ( \(x+y+z\))2 (đpcm)
⇒
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
= = = = = (1)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
= =
= ⇒ = ()2 (2)
Từ (1) và (2) ta có :
= + y2 + z2 = ( )2 (đpCm)

Áp dụng tính chất các dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}=\dfrac{x+y+z}{1}\)
\(x=a\left(x+y+z\right)=x^2=a^2.\left(x+y+z\right)^2\)
\(y=b\left(x+y+z\right)=y^2=b^2\left(x+y+z\right)^2\)
\(z=c\left(x+y+z\right)=z^2=c^2.\left(x+y+z\right)^2\)
\(\Rightarrow x^2+y^2+z^2=a^2\left(x+y+z\right)^2+b^2\left(x+y+z\right)^2+c^2\left(x+y+z\right)^2\)
\(=\left(x+y+z\right)^2\left(a^2+b^2+c^2\right)=\left(x+y+z\right)^2\) (do \(a^2+b^2+c^2=1\))
https://lazi.vn/edu/exercise/864720/cho-a-b-c-a2-b2-c2-1-va-x-a-y-b-z-c-chung-minh-rang-x-y-z2-x2-y2-z2
liệt phím? Mù mắt?

tham khảo
Ta có x:a=y:b=z:c=x+y+z:a+b+c=x+y+z( vì a+b+c=1)
do đó (x+y+z)^2=x^2:a^2=y^2:b^2=z^2:c^2=x^2+y^2+z^2:a^2+b^2+ c^2=x^2+y^2+z^2( vì a^2+b^2+c^2)
Vậy (x+y+z)^2=x^2+y^2+z^2

-Có: \(x:y:z=a:b:c\Rightarrow\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}=\dfrac{x+y+z}{2}\)
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\Rightarrow\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}=\dfrac{x^2+y^2+z^2}{2}\)
\(\Rightarrow\dfrac{\left(x+y+z\right)^2}{4}=\dfrac{x^2+y^2+z^2}{2}\)
\(\Rightarrow\left(x+y+z\right)^2=2x^2+2y^2+2z^2\left(đpcm\right)\)

VT−VP=a24+b2+c2−ab−bc+2bc+a212=(a2−b−c)2+a2−36bc12>0⇒VT−VP=a24+b2+c2−ab−bc+2bc+a212=(a2−b−c)2+a2−36bc12>0⇒ đpcm
Cách khác:
Từ giả thiết suy ra a>0a>0 và bc>0bc>0. Bất đẳng thức cần chứng minh tương đương với
a23+(b+c)2−3bc−a(b+c)≥0⟺13+(b+ca)2−b+ca−3a3≥0a23+(b+c)2−3bc−a(b+c)≥0⟺13+(b+ca)2−b+ca−3a3≥0
Vì a3>36a3>36 nên
13+(b+ca)2−b+ca−3a3>(b+ca)2−b+ca+14=(b+ca−12)2>0.Đây là bài 1