Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
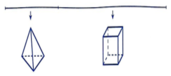
Gọi x là chiều dài đoạn thép thứ nhất, 0 < x < 10
=> Cạnh hình tứ diện là (tứ diện là đều)
Cạnh hình lập phương là 10 - x 12
Diện tích xung quanh của tứ diện là ![]()
Diện tích xung quanh của lập phương là ![]()
Tổng
S
1
+
S
2
đạt giá trị nhỏ nhất khi 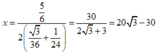
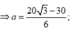
![]()
![]()

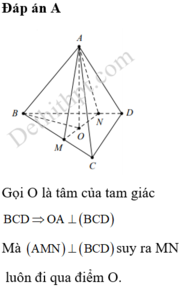
Đáp án D

Gọi O = AC ∩ BD
Vì ABCD là hình thoi nên AC ⊥ BD tại O.
Tam giác SBD cân tại S nên SO ⊥ BD.
Suy ra BD
⊥
(SAC)![]()
Do ![]() => SO = OC
=> SO = OC![]()
![]()
![]()
![]()
![]()
![]()
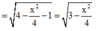
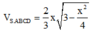
Đặt 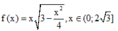
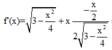
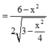
![]()
Bảng biến thiên:
| x |
0 |
|
|
+ 0 - |
|
|
|
Vậy ![]()

Đáp án C
Tứ diện ABCD có chiểu cao không đổi do đó thể tích nhỏ nhất khi diện tích tam giác ABC nhỏ nhất. Vì AB, BC, CA lần lượt tiếp xúc với quả cầu và phần quả cầu bên trong tứ diện có thể tích bằng phần quả cầu bên ngoài tứ diện nên tâm I của mặt cầu nằm trong tam giác ABC
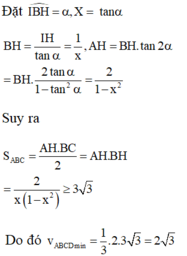
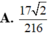
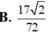
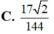
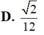

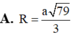
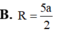
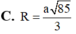
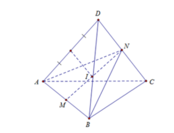

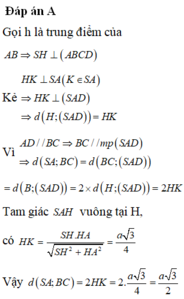
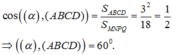
Đáp án D
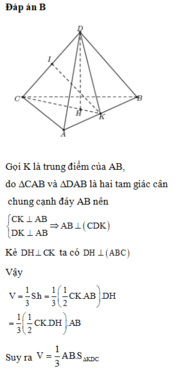
Gọi tứ diện đã cho là S. ABC. Ta có
Suy ra, V S . A B C đạt GTLN khi và chỉ khi sin ϕ = 1
=> Chọn phương án D.