Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

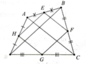
Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là: | D. Hình vuông. |
A. 4cm. B. 7cm. C. 14cm. Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là: | D. 8cm. |
A. 10cm. B. 15cm. C. 5cm. | D. 8cm. |
Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. D. Hình vuông.
Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
A. 4cm. B. 7 cm. C. 14cm. D. 8cm.
Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là:
A. 10cm. B. 15cm. C. 5cm. D. 8 cm

Do hình thang AEFD và hình thang BCFE có cùng đường cao, suy ra S A E F D = S B C F E ⇔ D F = A B + D C 2 − A E
Cách dựng: Vẽ đường trung bình MN, trên đó lấy MK = AE. Từ K vẽ đường song song với BC cắt CD tại F cần tìm

a) Hình chữ nhật \(ABCD\) có \(AB=CD=48 cm\), \(AD=BC=24 cm\).
\(M\) là trung điểm \(CD\) \(\Rightarrow CM=DM=\dfrac{CD}{2}=\dfrac{48}{2}=24\).
Kẻ \(MH\perp BF\Rightarrow MH=BC=24 cm\).
Ta có: \(S_{MBF}=\dfrac{1}{2}BF.MH\Rightarrow BF=\dfrac{2S_{MBF}}{MH}=\dfrac{2.468}{24}=39 (cm)\)
\(\Rightarrow AF=AB-BF=48-39=9 (cm)\).
b) Ta có:
\(S_{ADMF}=\dfrac{1}{2}(AF+DM).AD=\dfrac{1}{2}(9+24).24=396 (cm^2)\).
\(S_{BCMF}=\dfrac{1}{2}(BF+MC).BC=\dfrac{1}{2}(39+24).24=756 (cm^2)\).
ABCD là hcn = AB = CD = 48 cm; BC = AD = 24 cm.
M là trung điểm CD => MC = MD = 24 cm.
a) Ta thấy tam giác MBF có đường cao hạ từ M (gọi là MH) dài bằng đoạn DA = 24 cm (M thuộc CD, mà CD//AB, MH vuông góc với AB và DA cũng vuông góc với AB => MH = DA).
SMBF= MH.BF.1/2 = 468
24. BF. 1/2 = 468
BF = 40.5
AF = AB - BF = 7.5 (cm)
Vậy AF = 7.5 cm.
b) Hai tứ giác ADMF và BCMF là hai hình thang đó AF//DM và BF//CM.
SADMF= 1/2xADx(AF+DM)=1/2 x 24 x (7.5 + 24)
SBCMF= 1/2 x BC x (BF + CM) = 1/2 x 24 x (40.5 + 24)

Chứng minh EFGH là hình bình hành. Để EFGH là hình chữ nhật thì
Þ H E F ^ = 90 0 ⇒ H E ⊥ E F
Þ AC ^BD.

Giải
ABED là hình thang
SABED = \(\frac{1}{2}\)(48 + 24) . 24 = 864
AFED là hình thang. Gọi AF = x
SAFED = \(\frac{1}{2}\)(x + 24) . 24
= 12x + 288
Mặt khác SAFED = \(\frac{11}{24}\)SABED = \(\frac{864.11}{24}=396\)
Ta có 12x + 288 = 396 => x = 9
Chọn F trên cạnh AB sao cho AF = 9