Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
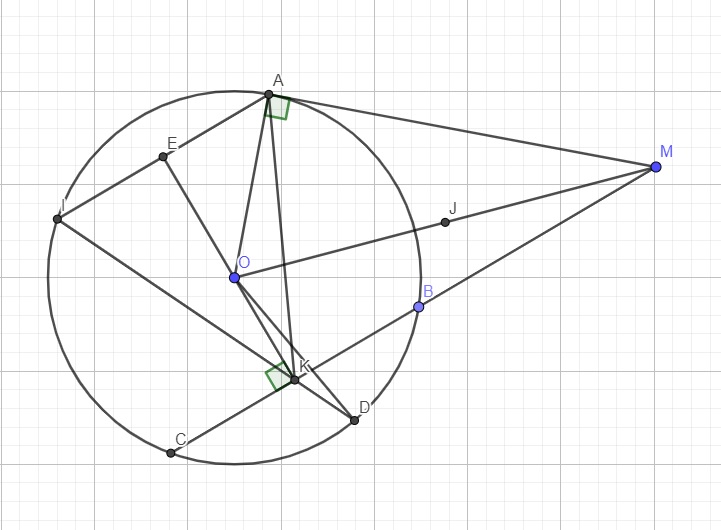
Do MA là tiếp tuyến \(\Rightarrow AM\perp OA\Rightarrow\Delta OAM\) vuông tại A
\(\Rightarrow O,A,M\) cùng thuộc đường tròn đường kính OM
Do \(OK\perp BC\Rightarrow\Delta OKM\) vuông tại K
\(\Rightarrow O,K,M\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow M,A,O,K\) cùng thuộc đường tròn đường kính OM
Hay tứ giác MAOK nội tiếp đường tròn đường kính OM, với tâm là trung điểm J của OM và bán kính \(R=\dfrac{OM}{2}\)
b.
Do \(AI||BC\Rightarrow\widehat{IAK}=\widehat{AKM}\) (so le trong)
Lại có MAOK nội tiếp \(\Rightarrow\widehat{AKM}=\widehat{AOM}\) (cùng chắn cung AM)
\(\Rightarrow\widehat{IAK}=\widehat{AOM}\) (1)
Mà \(\widehat{AOM}+\widehat{AMO}=90^0\) (\(\Delta OAM\) vuông tại A theo c/m câu a)
\(\Rightarrow\widehat{IAK}+\widehat{AMO}=90^0\)
c.
Gọi E là trung điểm AI \(\Rightarrow OE\perp IA\)
Mà \(IA||BC\Rightarrow OE\perp BC\Rightarrow O,E,K\) thẳng hàng
\(\Rightarrow KE\) đồng thời là đường cao và trung tuyến trong tam giác KAI
\(\Rightarrow\Delta KAI\) cân tại K \(\Rightarrow\widehat{AIK}=\widehat{IAK}\) \(\Rightarrow\widehat{AIK}=\widehat{AOM}\) (theo (1))
Mặt khác \(\widehat{AIK}\) và \(\widehat{AOD}\) là góc nội tiếp và góc ở tâm cùng chắn cung AD của (O)
\(\Rightarrow\widehat{AIK}=\dfrac{1}{2}\widehat{AOD}\Rightarrow\widehat{AOM}=\dfrac{1}{2}\left(\widehat{AOM}+\widehat{MOD}\right)\)
\(\Rightarrow\widehat{AOM}=\widehat{MOD}\)
Xét hai tam giác AOM và DOM có:
\(\left\{{}\begin{matrix}OM\text{ chung}\\\widehat{AOM}=\widehat{MOD}\left(cmt\right)\\AO=DO=R\end{matrix}\right.\) \(\Rightarrow\Delta AOM=\Delta DOM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODM}=\widehat{OAM}=90^0\)
\(\Rightarrow MD\) là tiếp tuyến của (O)
a) B,A,C,D nằm trên (O) => tg ABDC nt
góc NAB=90( góc nt chắn nửa (O))=> NA là đường cao tam giác BMN
Cmtt MD là đường cao tam giác BMN=> góc AMC=DNC ( cùng phụ góc ABD)
b) MD cắt AN tại C => C là trực tâm tam giác BMN => BC vuông góc MN tại H
c)Phần này mình nghĩ bạn làm được: Cm các tg DCHN,MHCA nt; sau đó cm tam giác MHC đồng dạng MDN, tam giác NHC đồng dạng tam giác NAM=> MC.MD=MH.MN;NC.NA=NH.MN
=> NC.NA+MC.MD=MH.MN+NH.MN=MN^2