Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a+b) Xét \(\Delta AFE\) và \(\Delta ACB:\)
Ta có:\(A\) là góc chung
AE=AB (gt)
AF=AC (gt)
Vậy \(\Delta AFE=\Delta ACB\)(c.g.c)
Vậy \(AFE=ACB\) góc tương ứng 1
Xét \(\Delta ABD\) và \(\Delta AED\)
Ta có : \(BAD=EAD\) ( gt )
AD là cạnh chung
AB=AE (cạnh tương ứng)
Vậy \(\Delta ABD=\Delta AED\) ( c.g.c)
Vậy BD=ED (cạnh tương ứng ) (2)
Xét \(\Delta BDF\) và \(\Delta EDC\)
Ta có: EC=BF ( Do EA=BA và AC=AF mà EC=AC-EA, BF=AF-AB )
Từ (1)(2)
Vậy \(\Delta BDF=\Delta EDC\) ( c.g.c)
c. Ta có: \(BDF=EDC\) ( góc đối, cm câu a)
Nên F, D, E thẳng hàng
d. AC=AF (cạnh tương ứng, cm trên)
Nên AD là đường phân giác đồng thời đường cao ứng \(\Delta ACF\) cân nên AD vuông góc FC

nguyễn triệu minh Xl : k cs ý j nhưng mà cs pk bạn cop bài tôi ??

a) Xét \(\Delta AFD;\Delta ADC\) có :
\(AF=AC\left(gt\right)\)
\(\widehat{FAD}=\widehat{CAD}\left(gt\right)\)
\(AD:chung\)
=> \(\Delta AFD=\Delta ADC\left(c.g.c\right)\)
=> \(FD=DE\) ( 2 cạnh tương ứng)
=> \(\widehat{AFD}=\widehat{ACD}\) ( 2 góc tương ứng)
Ta có : \(\left\{{}\begin{matrix}AB=AE\left(gt\right)\\AF=AC\left(gt\right)\end{matrix}\right.\)
Mà : \(\left\{{}\begin{matrix}AF=AB+FB\\AC=AE+EC\end{matrix}\right.\)
=> \(FB=EC\)
Xét \(\Delta BDF;\Delta EDC\) có :
\(FB=EC\left(cmt\right)\)
\(\widehat{BFD}=\widehat{ECD}\) (do \(\widehat{AFD}=\widehat{ACD}\) -cmt)
\(FD=CD\left(cmt\right)\)
=> \(\Delta BDF=\Delta EDC\left(c.g.c\right)\)
c) Từ \(\Delta BDF=\Delta EDC\left(cmt\right)\)
=> \(FD=DE\) ( 2 cạnh tương ứng)
=> D là trung điểm của EF
Do đó : F, D, E thẳng hàng (đpcm)
d) Xét \(\Delta AFC\) có :
\(AF=AC\left(gt\right)\)
=> \(\Delta AFC\) cân tại A
Mà có : AD là tia phân giác của \(\widehat{CAF}\)(gt)
=> AD đồng thời là đường trung trực trong \(\Delta AFC\)
Hay : \(AD\perp FC\left(đpcm\right)\)

Lời giải:
a) Ta có:
\(\left\{\begin{matrix} AB=AE\\ AF=AC\end{matrix}\right.\Rightarrow AF-AB=AC-AE\)
\(\Leftrightarrow BF=CE\) (1)
Xét tam giác $ADF$ và $ADC$ có:
\(\left\{\begin{matrix} AD -\text{chung}\\ \angle FAD=\angle CAD(\text{do AD là phân giác})\\ AF=AC\end{matrix}\right.\)
\(\Rightarrow \triangle ADF=\triangle ADC(c.g.c)\Rightarrow DF=DC\) (2)
Tương tự, ta cm đc \(\triangle ABD=\triangle AED(c.g.c)\Rightarrow BD=ED\) (3)
Từ \((1);(2);(3)\Rightarrow \triangle BDF=\triangle EDC\) (c.c.c)
b) Đã chứng minh ở phần a
c) Vì \(\triangle BDF=\triangle EDC(cmt)\Rightarrow \angle BDF=\angle EDC\)
\(\Rightarrow \angle BDF+\angle BDE=\angle EDC+\angle BDE\)
\(\Leftrightarrow \angle FDE=\angle BDC=180^0\Rightarrow F,D,E\) thẳng hàng
d)
Do $AF=AC$ nên tam giác $FAC$ cân tại $A$. Do đó đường phân giác $AD$ đồng thời cũng là đường cao ứng với cạnh đáy $FC$ (tính chất của tam giác cân)
\(\Rightarrow AD\perp FC\) (đpcm)

Gửi em
Câu a và câu b (Đề bài có chút ngược ngược :<)
Xét \(\Delta ABD\) và \(\Delta ADE\) có :
AD : cạnh chung
\(\widehat{BAD}=\widehat{DAE}\) ( AD là tia phân giác của \(\widehat{BAC}\) )
AB = AE (gt)
=> \(\Delta ABD=\Delta ACD\left(c.g.c\right)\)
Xét \(\Delta ADF\) và \(\Delta ADC\) có :
AD : cạnh chung
\(\widehat{BAD}=\widehat{DAE}\) ( AD là tia p/g của \(\widehat{BAC}\) )
AC = AF (gt)
=> \(\Delta ADF\) = \(\Delta ACF\) ( c.g.c )
+ Ta có :
BF = AF - AB
EC = AC - AE
Mà : AB = AE , AF = AC
=> BF = EC
Xét \(\Delta BDF\) và \(\Delta EDC\) ,có :
BD = ED ( \(\Delta ABD=\Delta AED\) )
BF = EC ( cmt )
FD = CD ( \(\Delta ADF=\Delta ADC\) )
=> \(\Delta BDF=\Delta EDC\left(c.c.c\right)\)
Câu c)
Ta có :
=> ΔBDF = \(\Delta\)EDF ( cm câu a )
=> \(\widehat{BDF}=\widehat{EDC}\) ( 2 góc tương ứng )
Mà chúng là hai góc ở vị trí đối đỉnh
=> Ba điểm E , D , F thẳng hàng
Câu d)
Xét \(\Delta\)AIF và \(\Delta\)AIC ,có :
AI : là cạnh chung
AF = AC (gt)
\(\widehat{FAD}=\widehat{CAD}\) ( AD là tia tia ph/g của góc BAC )
=> \(\Delta\)AIF = \(\Delta AIC\left(c.g.c\right)\)
=> \(\widehat{FIA}\) = \(\widehat{CIA}\)
Mà \(\widehat{FIA}\) + \(\widehat{CIA}\)= 1800
=> \(\widehat{FIA}\) = \(\widehat{CIA}\) = \(\dfrac{180^0}{2}=90^0\) Vậy AI \(\perp FC\) hay AD \(\perp FC\)Bạn tham khảo tại đây nhé: https://hoc24.vn/hoi-dap/question/203636.html
Chúc bạn học tốt!

Mình nghĩ bạn nên thêm những ký hiệu bằng á bạn, ví dụ như là AC=AF,...
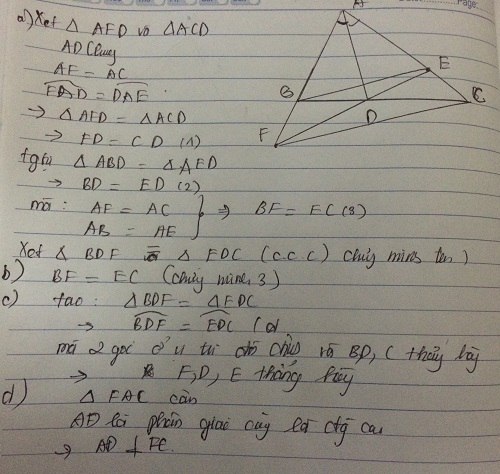


△ABC: AB < AC. BAD = DAC = BAC/2 (D BC)
BC)
E AC : AE = AB
AC : AE = AB
F AB : AF = AC
AB : AF = AC
a, △ABD = △AED
b, AD ⊥ FC
c, △BDF = △EDC ; BF = EC
d, F, D, E thẳng hàng
Bài làm:
a, Xét △ABD và △AED
Có: AB = AE (gt)
BAD = DAE (gt)
AD là cạnh chung
=> △ABD = △AED (c.g.c)
b, Vì △ABD = △AED (cmt)
=> BD = ED (2 cạnh tương ứng)
=> D thuộc đường trung trực của BE (1)
Vì AB = AE (gt) => A thuộc đường trung trực của BE (2)
Từ (1) và (2) => AD là đường trung trực của BE
=> AD ⊥ FC
c, Vì △ABD = △AED (cmt)
=> ABD = AED (2 góc tương ứng)
Ta có: ABD + DBF = 180o (2 góc kề bù)
AED + DEC = 180o (2 góc kề bù)
Mà ABD = AED (cmt)
=> DBF = DEC
Lại có: AB + BF = AF
AE + EC = AC
Mà AB = AE (gt) ; AF = AC (gt)
=> BF = EC
Xét △BDF và △EDC
Có: BD = ED (cmt)
DBF = DEC (cmt)
BF = EC (cmt)
=> △BDF = △EDC (c.g.c)
d, Vì △BDF = △EDC (cmt)
=> BDF = EDC (2 góc tương ứng)
Ta có: BDE + EDC = 180o (2 góc kề bù)
=> BDE + BDF = 180o
=> FDE = 180o
=> 3 điểm F, D, E thẳng hàng