Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a+b) Xét \(\Delta AFE\) và \(\Delta ACB:\)
Ta có:\(A\) là góc chung
AE=AB (gt)
AF=AC (gt)
Vậy \(\Delta AFE=\Delta ACB\)(c.g.c)
Vậy \(AFE=ACB\) góc tương ứng 1
Xét \(\Delta ABD\) và \(\Delta AED\)
Ta có : \(BAD=EAD\) ( gt )
AD là cạnh chung
AB=AE (cạnh tương ứng)
Vậy \(\Delta ABD=\Delta AED\) ( c.g.c)
Vậy BD=ED (cạnh tương ứng ) (2)
Xét \(\Delta BDF\) và \(\Delta EDC\)
Ta có: EC=BF ( Do EA=BA và AC=AF mà EC=AC-EA, BF=AF-AB )
Từ (1)(2)
Vậy \(\Delta BDF=\Delta EDC\) ( c.g.c)
c. Ta có: \(BDF=EDC\) ( góc đối, cm câu a)
Nên F, D, E thẳng hàng
d. AC=AF (cạnh tương ứng, cm trên)
Nên AD là đường phân giác đồng thời đường cao ứng \(\Delta ACF\) cân nên AD vuông góc FC

| GT | △ABC: AB < AC. BAD = DAC = BAC/2 (D E F |
| KL | a, △ABD = △AED b, AD ⊥ FC c, △BDF = △EDC ; BF = EC d, F, D, E thẳng hàng |
Bài làm:
a, Xét △ABD và △AED
Có: AB = AE (gt)
BAD = DAE (gt)
AD là cạnh chung
=> △ABD = △AED (c.g.c)
b, Vì △ABD = △AED (cmt)
=> BD = ED (2 cạnh tương ứng)
=> D thuộc đường trung trực của BE (1)
Vì AB = AE (gt) => A thuộc đường trung trực của BE (2)
Từ (1) và (2) => AD là đường trung trực của BE
=> AD ⊥ FC
c, Vì △ABD = △AED (cmt)
=> ABD = AED (2 góc tương ứng)
Ta có: ABD + DBF = 180o (2 góc kề bù)
AED + DEC = 180o (2 góc kề bù)
Mà ABD = AED (cmt)
=> DBF = DEC
Lại có: AB + BF = AF
AE + EC = AC
Mà AB = AE (gt) ; AF = AC (gt)
=> BF = EC
Xét △BDF và △EDC
Có: BD = ED (cmt)
DBF = DEC (cmt)
BF = EC (cmt)
=> △BDF = △EDC (c.g.c)
d, Vì △BDF = △EDC (cmt)
=> BDF = EDC (2 góc tương ứng)
Ta có: BDE + EDC = 180o (2 góc kề bù)
=> BDE + BDF = 180o
=> FDE = 180o
=> 3 điểm F, D, E thẳng hàng

a) Xét tam giác ABD và tam giác AED có:
AB=AE (GT)
góc BAD = góc EAD (AD là tia phân giác)
AD chung
Suy ra tam giác ABD=tam giác AED(CGC)
Suy ra BD=BE (hai cạnh tương ứng)
Xét tam giác AFD và tam giác ACD có:
AF=AC(GT)
Góc FAD= góc CAD (AD là tia phân giác của góc A)
AD chung
suy ra tam giác AFD và tam giác ACD(CGC)
suy ra DF=DC(2 cạnh tương ứng)
vì AB+BF=AE+EC (AF=AC)
Mà AB=AE(GT)
Suy ra BF=EC
Xet tam giác BFD và tam giác ECD có:
DB=DE(CMT)
DF=DC(CMT)
BF=EC(CMT)
Suy ra tam giac BFD=tamgiác ECD (CCC)
b) BF=EC (CMT)
c) vì tam giác BFD=tam giác ECD (CMT)
Suy ra gócBDF= gócEDC(2 GÓC TƯƠNG ỨNG)
Mà 2 góc này ở vị trí đối đỉnh
suy ra 3 điểm F,D,E thẳng hàng
d) xét tam giác AFD có:
AF=EC(GT)
Suy ra tam giác AFC cân tại A
mà AD là tia phân giac của góc A(gt)
suy ra AD cũng là đường cao của tam giác FAC
hay AD vuông góc FC
 BC)
BC)
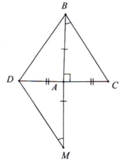
Mình nghĩ bạn nên thêm những ký hiệu bằng á bạn, ví dụ như là AC=AF,...