Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(MA=5\leftrightarrow x^2+\left(y-1\right)^2=5^2\)
Thay tọa độ điểm x,y vào tham số t vào pt trên ta được :
\(\left(2+2t\right)^2+\left(3+t-1\right)^2=25\)
\(\Leftrightarrow4t^2+8t+4+4+4t+t^2=25\)
\(\Leftrightarrow5t^2+12t-17=0\rightarrow t_1=1;t_2=-\dfrac{17}{5}\)
Với \(t_1=1\), ta được điểm \(x=4;y=4\Rightarrow M_1\left(4;4\right)\)
Với \(t_2=-\dfrac{17}{5}\)ta được điểm \(x=-\dfrac{24}{5};y=-\dfrac{2}{5}\Rightarrow M_2\left(-\dfrac{24}{5};-\dfrac{2}{5}\right)\)

Do M thuộc d nên tọa độ có dạng \(M\left(3m+2;m+3\right)\)
\(\Rightarrow\overrightarrow{AM}=3m-7;m+2\)
\(AM=5\Leftrightarrow\sqrt{\left(3m-7\right)^2+\left(m+2\right)^2}=5\)
\(\Leftrightarrow10m^2-38m+28=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\frac{14}{5}\end{matrix}\right.\)
Có 2 điểm M thỏa mãn

Do M thuộc (d) nên gọi tọa độ M có dạng: \(\left(1+2m;-3+3m\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(2m+1;3m-4\right)\)
Mà AM=5
\(\Leftrightarrow\left(2m+1\right)^2+\left(3m-4\right)^2=25\)
\(\Leftrightarrow13m^2-20m-8=0\) \(\Rightarrow m=\frac{10\pm2\sqrt{51}}{13}\)
Số xấu quá

Bạn thay vào vecto AM à? Mình tưởng phải thay vào điểm M chứ.
Bài 1:
Do M thuộc d nên tọa độ M có dạng \(M\left(a;\frac{2a+4}{3}\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(a;\frac{2a+1}{3}\right)\)
Mà \(AM=5\Leftrightarrow a^2+\left(\frac{2a+1}{3}\right)^2=25\)
\(\Leftrightarrow13a^2+4a-224=0\Rightarrow\left[{}\begin{matrix}a=4\\a=-\frac{56}{13}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}M\left(4;\frac{9}{3}\right)\\M\left(-\frac{56}{13};-\frac{20}{13}\right)\end{matrix}\right.\)
Câu 2:
Do (C) tiếp xúc \(\Delta\Leftrightarrow R=d\left(C;\Delta\right)\)
\(\Rightarrow R=\frac{\left|-2.5-12.2-10\right|}{\sqrt{5^2+12^2}}=\frac{44}{13}\)

Đáp án: A

Vì d vuông góc với d’ nên d sẽ nhận vecto chỉ phương của d’ làm vecto pháp tuyến
Vậy d là đường thẳng đi qua M và có vecto pháp tuyến là 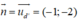
d: -1(x - 2) - 2(y + 3) = 0 ⇔ -x - 2y - 4 ⇔ x + 2y + 4 = 0

M thuộc d nên tọa độ có dạng:
\(M\left(t+3;t+2\right)\) với \(t>-3\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|2\left(t+3\right)-\left(t+2\right)-3\right|}{\sqrt{2^2+\left(-1\right)^2}}=2\sqrt{5}\)
\(\Leftrightarrow\left|t+1\right|=10\Rightarrow\left[{}\begin{matrix}t=9\\t=-11\left(l\right)\end{matrix}\right.\)
\(\Rightarrow M\left(12;11\right)\)

Do I thuộc d nên tọa độ có dạng: \(I\left(1+t;2+t\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(1+t;t+5\right)\\\overrightarrow{OI}=\left(1+t;2+t\right)\end{matrix}\right.\)
Do tam giác AIO vuông tại I nên \(AI\perp OI\)
\(\Rightarrow\overrightarrow{AI}.\overrightarrow{OI}=0\)
\(\Rightarrow\left(1+t\right)^2+\left(t+2\right)\left(t+5\right)^2=0\)
\(\Leftrightarrow2t^2+9t+11=0\)
Pt trên vô nghiệm nên ko tồn tại điểm I thỏa mãn yêu cầu đề bài
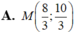
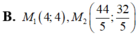
Lấy điểm M( 2+ 2t; 3+ t) nằm trên d;
Để AM= 5 khi và chỉ khi
(2t+2) 2+ (t+2) 2= 25 hay 5t2+12t- 17= 0
Suy ra t= 1 hoặc t= - 17/5
Với t= 1 thì M( 4;4)
Chọn C.