WO
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TG
14 tháng 1 2021
Ta có
ax^3 + by^3 = (x + y)(ax^2 + by^2) - xy(ax + by)
=> 9 = 5(x + y) - 3xy (1)
ax^4 + by^4 = (x + y)(ax^3 + by^3) - xy(ax^2 + by^2)
=> 17 = 9(x + y) - 5xy (2)
Từ (1) và (2) => x + y = 3 và xy = 2
=> x, y là nghiệm của pt ∝^2 - 3∝ + 2 = 0 (∝ - 1)(∝ - 2) = 0 ∝ = 1 hoặc ∝ = 2
=> (x , y) = (1 ; 2) hoặc (2 ; 1)
Không mất tính tổng quát, giả sử (x , y) = (1 ; 2)
Giả thiết ban đầu a + 2b = 3; a + 4b = 5 ; a + 8b = 9 ; a + 16b = 17
=> a = b = 1
Vậy ax^2001 + by^2001 = 1.1^2001 + 1.2^2001 = 1 + 2^2001
TG
14 tháng 1 2021
Ta có
ax^3 + by^3 = (x + y)(ax^2 + by^2) - xy(ax + by)
=> 9 = 5(x + y) - 3xy (1)
ax^4 + by^4 = (x + y)(ax^3 + by^3) - xy(ax^2 + by^2)
=> 17 = 9(x + y) - 5xy (2)
Từ (1) và (2) => x + y = 3 và xy = 2
=> x, y là nghiệm của pt ∝^2 - 3∝ + 2 = 0 (∝ - 1)(∝ - 2) = 0 ∝ = 1 hoặc ∝ = 2
=> (x , y) = (1 ; 2) hoặc (2 ; 1)
Không mất tính tổng quát, giả sử (x , y) = (1 ; 2)
Giả thiết ban đầu a + 2b = 3; a + 4b = 5 ; a + 8b = 9 ; a + 16b = 17
=> a = b = 1
Vậy ax^2001 + by^2001 = 1.1^2001 + 1.2^2001 = 1 + 2^2001
HP
0
DV
0
CM
6 tháng 6 2018
* Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
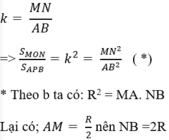
Mà: MN = MP+NP = MA+NB = R/2 +2R = 5R/2
H
25 tháng 3 2020
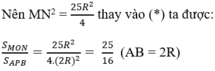
a, Ta có: AC = CM (tinhs chất 2 tt cắt nhau)
BD = DM (tính chất 2 tiếp tuyến cắt nhau)
Mà CD = CM + DM
=> CD = AC + BD (đpcm)
Lại có: \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}=180^o\)
mà \(\widehat{O_1}=\widehat{O_2};\widehat{O_3}=\widehat{O_4}\) (t/c 2 tiếp tuyến cắt nhau)
=> \(2\left(\widehat{O_2}+\widehat{O_3}\right)=180^o\Rightarrow\widehat{O_2}+\widehat{O_3}=90^o\) hay \(\widehat{COD}=90^o\) (đpcm)
b, Ta có: \(AC\perp AB;BD\perp AB\) => AC // BD
Xét \(\Delta BND\) có: AC//BD
=> \(\frac{CN}{BN}=\frac{AC}{BD}\) (hệ quả định lý Talet)
Mà AC = CM ; BD = DM (cmt)
=> \(\frac{CN}{BN}=\frac{CM}{DM}\)
Xét \(\Delta BCD\) có: \(\frac{CN}{BN}=\frac{CM}{DM}\)
=> MN // BD (đpcm)
nks
- Gọi P=x+y và Q=xy
- Áp dụng công thức (ax^n + by^n)(x + y) = (ax^n+1 + by^n+1) + xy(ax^n-1 + by^n-1)
* n=1 ta có:
(ax + by)(x + y) = (ax^2 + by^2) + xy(ax^0 + by^0)
=> 10P = 24 + 6Q <=> 5P = 12 + 3Q (1)
* n=2 ta có:
(ax^2 + by^2)(x + y) = (ax^3 + by^3) + xy(ax + by)
=> 24P = 62 + 10Q <=> 12P = 31 + 5Q (2)
Từ (1) và (2) suy ra: P=3 ; Q=1
Ta có: M = ax^4 + by^4
= ax^4 + bxy^3 + ayx^3 + by^4 - bxy^3 - ayx^3
= x(ax^3 + by^3) + y(ax^3 + by^3) - xy(by^2 + ax^2)
= (ax^3 + by^3)(x + y) - xy(by^2 + ax^2)
=> M = 62 . 3 - 24 = 162
Vậy M = 162
gửi nhầm bài nên tự lm luôn, Mọi ng thông cảm ^^