K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
14.
Hàm số ko xác định tại \(x=-1,x=2\) nên gián đoạn tại \(x=-1,x=2\)
A đúng
15.
\(\lim\limits_{x\rightarrow1^-}\dfrac{2x+1}{x-1}=-\infty\)
(Do \(\lim\limits_{x\rightarrow1^-}\left(2x+1\right)=3>0\) và \(x-1< 0\) khi \(x< 1\))
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
DN
0
VV
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
9.
Gọi D là trung điểm BC \(\Rightarrow AD\perp BC\) (do tam giác ABC đều)
Mặt khác \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAD\right)\)
Mà BC là giao tuyến (SAB) và (SBC)
\(\Rightarrow\widehat{SDA}\) là góc giữa (ABC) và (SBC)
\(AD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{1}{\sqrt{3}}\)
\(\Rightarrow\widehat{SDA}=30^0\)
b.
Câu b nhìn không rõ, đề yêu cầu tính diện tích tam giác SBC đúng không nhỉ?
Từ câu a ta có \(BC\perp\left(SAD\right)\Rightarrow SD\perp BC\)
Pitago tam giác SAD: \(SD=\sqrt{SA^2+AD^2}=a\)
\(\Rightarrow S_{\Delta SBC}=\dfrac{1}{2}SD.BC=\dfrac{a^2}{2}\)
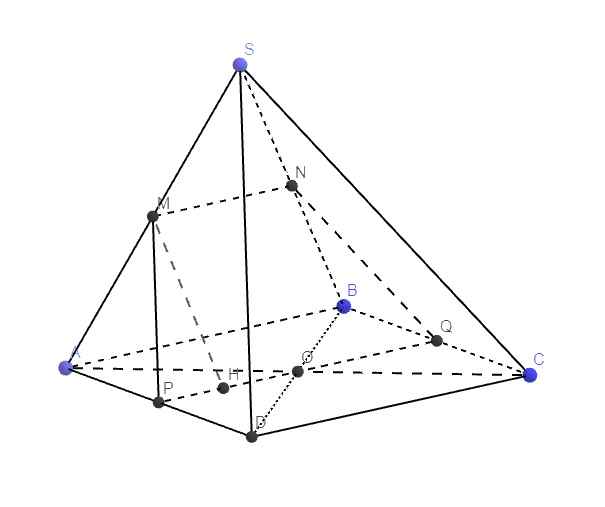
a.
Ta có: \(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(S=\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Do \(AB||CD\Rightarrow\) giao tuyến của (SAC) và (SBD) là một đường thẳng song song AB và CD
Qua S kẻ đường thẳng \(d||AB\)
Do \(S=\left(SAB\right)\cap\left(SCD\right)\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
\(O\in AC\in\left(AMC\right)\Rightarrow OM\in\left(AMC\right)\)
\(\left\{{}\begin{matrix}M\in SB\\O\in BD\end{matrix}\right.\) \(\Rightarrow OM\in\left(SBD\right)\) \(\Rightarrow OM=\left(AMC\right)\cap\left(SBD\right)\)
Trong mp (SBD), kéo dài OM cắt SD tại Q
\(\Rightarrow Q=SD\in\left(AMC\right)\)
c.
Gọi E là trung điểm SA
Do G là trọng tâm tam giác SAB \(\Rightarrow G\in BE\) và \(BG=\dfrac{2}{3}BE\Rightarrow\dfrac{BG}{BE}=\dfrac{2}{3}\) (1)
Do \(AB||CD\) , áp dụng định lý Talet: \(\dfrac{OD}{OB}=\dfrac{CD}{AB}=\dfrac{1}{2}\Rightarrow\dfrac{OD}{OB}+1=\dfrac{3}{2}\Rightarrow\dfrac{OD+OB}{OB}=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{BD}{OB}=\dfrac{3}{2}\Rightarrow\dfrac{BO}{BD}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow\dfrac{BG}{BE}=\dfrac{BO}{BD}\Rightarrow OG||ED\) (Talet đảo)
Mà \(ED\in\left(SAD\right)\Rightarrow OG||\left(SAD\right)\)