
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


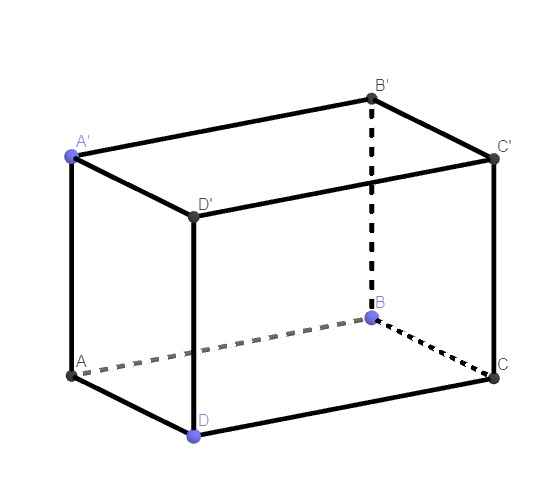
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)


Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)

1.
c, \(sin\left(\dfrac{\pi}{3}-x\right)=-\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}-x=arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\\dfrac{\pi}{3}-x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\x=-\dfrac{2\pi}{3}+arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
d, \(sin4x=\dfrac{2}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=arcsin\dfrac{2}{3}+k2\pi\\4x=\pi-arcsin\dfrac{2}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\end{matrix}\right.\)
1.
e, \(2sin2x+\sqrt{2}=0\)
\(\Leftrightarrow sin2x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin2x=sin\left(-\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{8}+k\pi\\x=\dfrac{5\pi}{8}+k\pi\end{matrix}\right.\)

Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)

\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)
Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)
\(\left(sinx+cosx\right)'=cosx-sinx\)
Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)

Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF

\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)

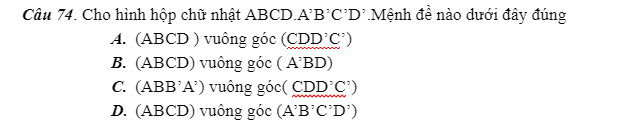
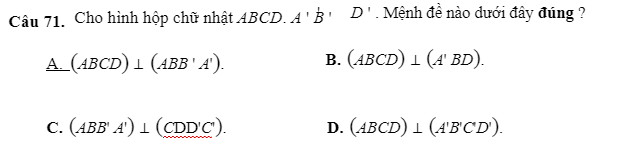






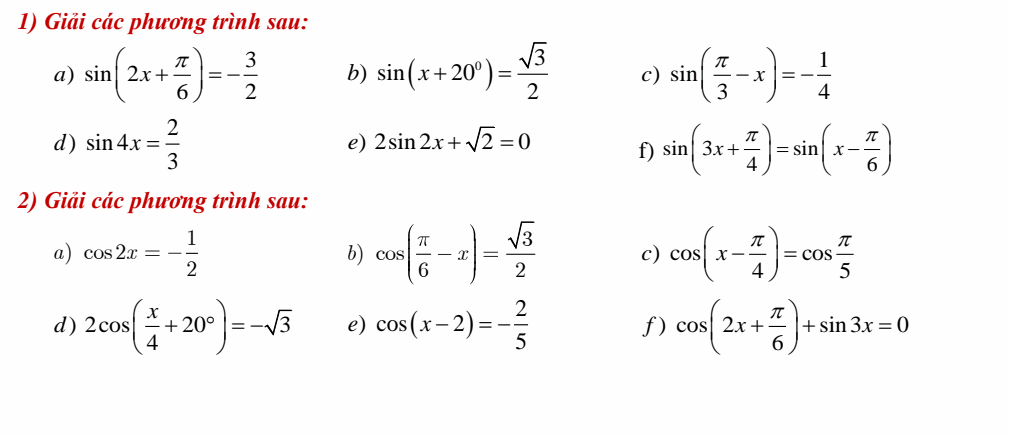




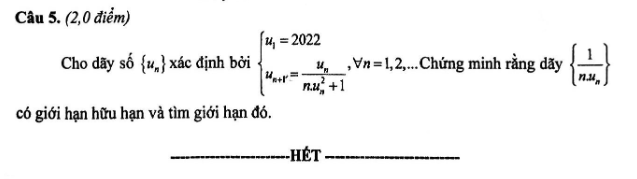 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ