Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

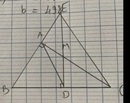
a: Xét ΔCDM vuông tại D và ΔCAB vuông tại A có
góc C chung
=>ΔCDM đồng dạng với ΔCAB
b: Xét ΔMAE vuông tại A và ΔMDC vuông tại D có
góc AME=góc DMC
=>ΔMAE đồng dạng với ΔMDC
=>MA/MD=ME/MC
=>MA*MC=MD*ME
c: góc CAE=góc CDE=90 độ
=>CDAE nội tiếp
=>góc MAD=góc MEC

Hình Tự kẻ
Xét Tam giác ABC và Tam giác DBE có : BAC = BDE ; ABC = DBE
Từ Tam giác ABC và Tam giác DBE đồng dạng suy ra góc C = Góc E
Xét Tam giác MDC và MAE (đồng dạng ) suy ra MA / MD = ME / MC , suy ra MA.MC=MD.ME
Xét tam giác MAD và Tam giác MCE có : AMD = CME ; MA/MD=ME/MC , Suy ra Tam giác MAD đồng dạng với Tam giác MEC
a, Xét tam giác ABC và tam giác DBE có :
góc B chung
góc BAC = góc BDE (=90độ )
Do đó : tam giác ABC đồng dạng với tam giác DBE ( g.g )
b, Xét tam giác MAE và tam giác MDC có :
góc MAE = góc MDC ( = 90độ )
góc AME = góc DMC ( đối đỉnh )
Do đó : tam giác MAE đồng dạng với tam giác MDC ( g.g )
\(\Rightarrow\frac{MA}{MD}=\frac{ME}{MC}\)
\(\Rightarrow MA.MC=MD.ME\)
c,d : Tự làm nốt nhé , em mới lớp 7 nên đến đây chịu ạ .
Học tốt

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF