Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(BH^2=HA\cdot HC\)
\(\Leftrightarrow BH^2=2\cdot6=12\)
hay \(BH=2\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBHA vuông tại H, ta được:
\(BA^2=BH^2+HA^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{3}\right)^2+2^2=12+4=16\)
hay BA=4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow BC^2=8^2-4^2=48\)
hay \(BC=4\sqrt{3}\left(cm\right)\)
b) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{CA}=\dfrac{4\sqrt{3}}{8}=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{A}=\dfrac{BA}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)

Gọi \(O\) là giao điểm của trục của hình thang cân \(ABCD\) và đường trung trực của cạnh bên \(AD\). Sử dụng tính chất: Điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó chứng minh \(OA=OB=OC=OD\).
Gọi O=d∩d′O ta có:
\(d\) là trục của hình thang cân \(ABCD\)⇒ d là đường trung trực của AB và CD.
Mà \(O\) ∈ \(d\)⇒{\(OA=OB\)
\(OC=OD\) (1)
(điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó).
Lại có \(O\) ∈ \(d'\)⇒\(OA=OD\) (2)
(điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó).
Từ (1) và (2) ⇒ \(OA=OB=OC=OD\)
Vậy bốn điểm \(A,B,C,D\)cùng thuộc đường tròn tâm \(O\), bán kính \(R=OA=OB=OC=OD\).
Ta có: ABCD là hình thang cân
nên \(\widehat{A}=\widehat{B};\widehat{C}=\widehat{D}\)
hay \(\widehat{A}+\widehat{C}=180^0\)
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn

A= \(\frac{1}{3}\left(\frac{1}{1.2.3}-\frac{1}{2.3.4}+\frac{1}{2.3.4}-\frac{1}{3.4.5}+\frac{1}{3.4.5}-\frac{1}{4.5.6}+...+\frac{1}{19.20.21}-\frac{1}{20.21.22}\right)\)
=\(\frac{1}{3}\left(\frac{1}{6}-\frac{1}{9240}\right)\)
=\(\frac{171}{3080}\)
A=1/1-1/2-1/3+1/2-1/3-1/4-1/5+1/3-1/4-1/5-1/6+...+1/19-1/20-1/21-1/22
A=1/1-1/22
A=21/22
Vậy A=21/22

Dòng một chiều DC là dòng điện có biên độ không thay đổi cực tính theo thời gian. Hay nói cách khác: đồ thị dòng điện luôn nằm 1 phía so với trục thời gian.
Dòng xoay chiều AC là dòng điện có cường độ biến thiên điều hòa theo thời gian theo hàm sin hoặc cos
Độ lớn dòng điện
- Dòng AC : Cường độ biến thiên điều hòa theo thời gian
- Dòng DC : Gần như là hằng số
Từ trường
Là dạng vật chất tồn tại xung quanh hạt mang điện chuyển động (dòng điện) hay các nam châm. Do đó nó sẽ tùy thuộc vào độ lớn và chiều của dòng điện.
- Dòng AC : Biến thiên theo thời gian
- Dòng DC : Không đổi
Đặc trưng cản trở dòng
- Dòng AC : Trở kháng (tổng trở)

a) 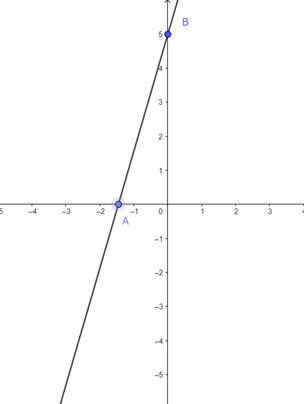
b) \(tanOAB=\dfrac{OB}{OA}=\dfrac{5}{\dfrac{5}{3}}=3\Rightarrow\widehat{OAB}=71^o34'\)

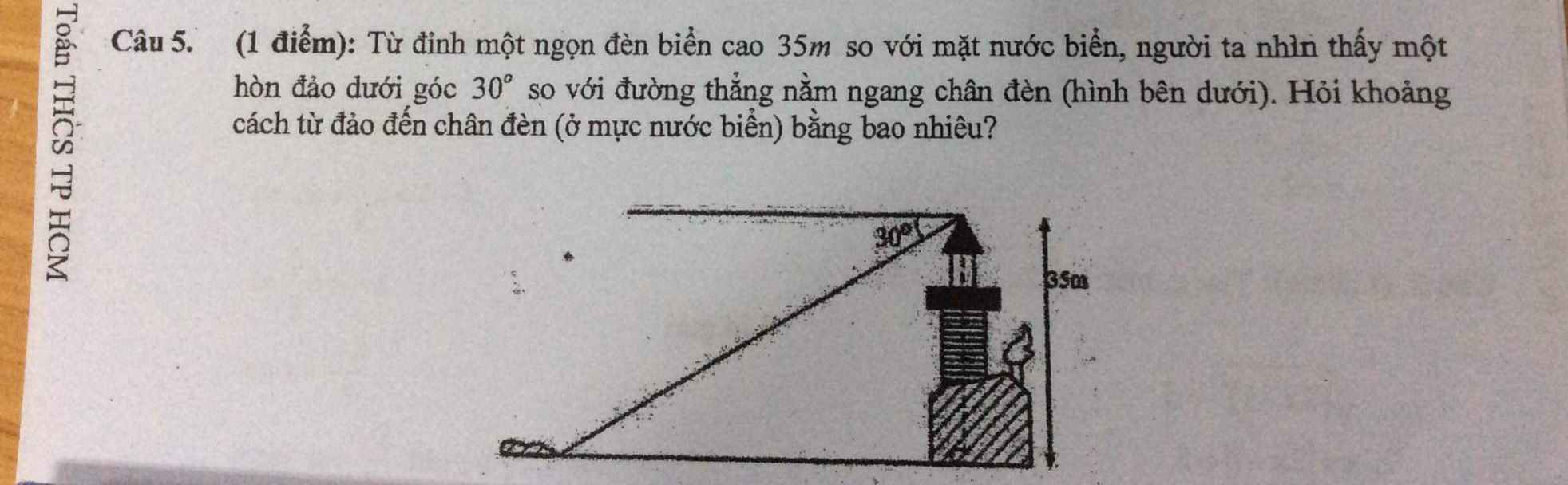
Ta coi hình vẽ là tam giác ABC vuông tại A với B là đỉnh ngọn đèn
góc BCA=30o(2 góc so le trong)
Theo tỉ số lượng giác trong tam giác vuông ta có:
CA=AB : tanC30
CA=35:tan30=60,6(m)
Vậy khoảng cách từ chân đèn đến hòn đảo là 60,6m

Bài 2:
a) Để hàm số đồng biến thì m+1>0
hay m>-1
b) Để hàm số đi qua điểm A(2;4) thì
Thay x=2 và y=4 vào hàm số, ta được:
\(\left(m+1\right)\cdot2=4\)
\(\Leftrightarrow m+1=2\)
hay m=1
c) Để hàm số đi qua điểm B(2;-4) thì
Thay x=2 và y=-4 vào hàm số, ta được:
\(2\left(m+1\right)=-4\)
\(\Leftrightarrow m+1=-2\)
hay m=-3
Bài 1:
b) Ta có: \(5\cdot\sqrt{25a^2}-25a\)
\(=5\cdot5\cdot\left|a\right|-25a\)
\(=-25a-25a=-50a\)


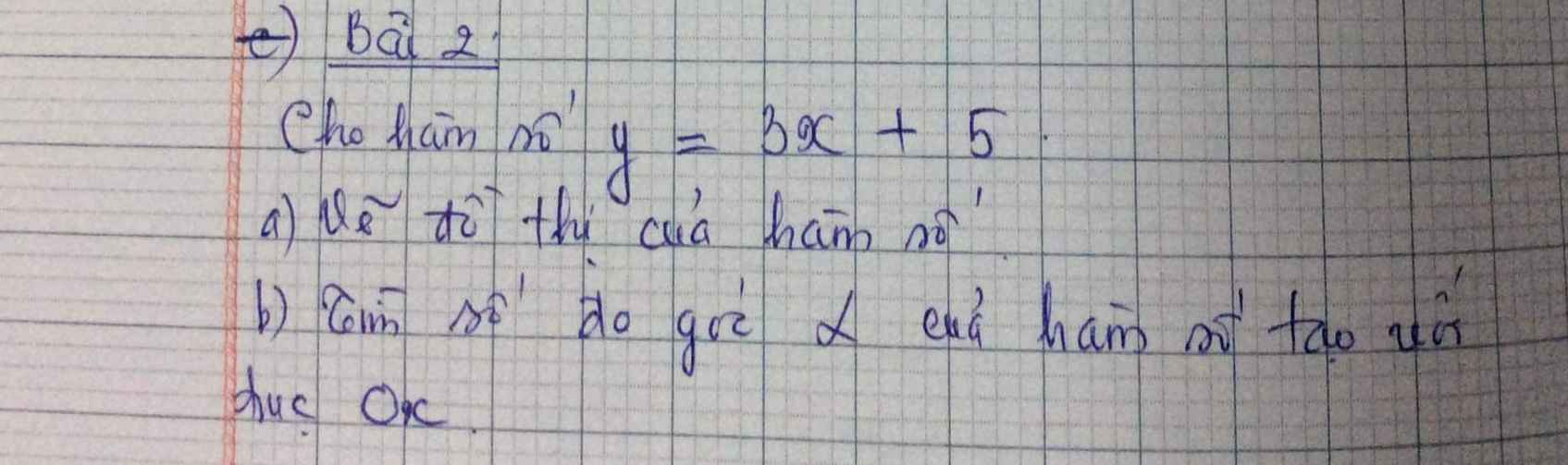

a)\(\frac{1}{n\left(n+1\right)\left(n+2\right)}=\frac{1}{2}.\frac{1}{n+1}.\left(\frac{1}{n}-\frac{1}{n+2}\right)\)=\(\frac{1}{2}.\frac{1}{n\left(n+1\right)}-\frac{1}{2}.\frac{1}{\left(n+1\right)\left(n+2\right)}\)= \(\frac{1}{2}\left(\frac{1}{n}-\frac{1}{n+1}\right)-\frac{1}{2}\left(\frac{1}{n+1}-\frac{1}{n+2}\right)\)
=> a = \(\frac{1}{2}\left(\frac{1}{1}-\frac{1}{2}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{3}\right)\)+\(\frac{1}{2}\left(\frac{1}{2}-\frac{1}{3}\right)-\frac{1}{2}\left(\frac{1}{3}-\frac{1}{4}\right)\)+....+\(\frac{1}{2}\left(\frac{1}{2018}-\frac{1}{2019}\right)-\frac{1}{2}\left(\frac{1}{2019}-\frac{1}{2020}\right)\)=\(\frac{1}{2}\left(1-\frac{1}{2}\right)-\frac{1}{2}\left(\frac{1}{2019}-\frac{1}{2020}\right)\)=\(\frac{1}{4}\left(1-\frac{1}{2019.1010}\right)\)=\(\frac{2019.1010-1}{2.2019.2020}\)
b) tương tự \(\frac{1}{n\left(n+1\right)\left(n+2\right)\left(n+3\right)}=\left(\frac{1}{n}-\frac{1}{n+1}\right)\left(\frac{1}{n+2}-\frac{1}{n+3}\right)\)=\(\frac{1}{2}\left(\frac{1}{n}-\frac{1}{n+2}\right)-\left(\frac{1}{n+1}-\frac{1}{n+2}\right)\)-\(\frac{1}{3}\left(\frac{1}{n}-\frac{1}{n+3}\right)+\frac{1}{2}\left(\frac{1}{n+1}-\frac{1}{n+3}\right)\)=\(\frac{1}{6}\left(\frac{1}{n}-\frac{1}{n+1}\right)-\frac{1}{3}\left(\frac{1}{n+1}-\frac{1}{n+2}\right)\)+\(\frac{1}{6}\left(\frac{1}{n+2}-\frac{1}{n+3}\right)\)= M-P+N
Với n từ 1 đến 2017 thì
M= \(\frac{1}{6}\left(\frac{1}{1}-\frac{1}{2}\right)+\frac{1}{6}\left(\frac{1}{2}-\frac{1}{3}\right)+...\)+\(\frac{1}{6}\left(\frac{1}{2017}-\frac{1}{2018}\right)\)=\(\frac{1}{6}\left(1-\frac{1}{2018}\right)=\frac{2017}{6.2018}\)
N= \(\frac{1}{6}\left(\frac{1}{3}-\frac{1}{4}\right)+\frac{1}{6}\left(\frac{1}{4}-\frac{1}{5}\right)+...+\)\(\frac{1}{6}\left(\frac{1}{2019}-\frac{1}{2020}\right)=\)\(\frac{1}{6}\left(\frac{1}{3}-\frac{1}{2020}\right)=\frac{2017}{6.3.2020}\)
P= \(\frac{1}{3}\left(\frac{1}{2}-\frac{1}{3}\right)+\frac{1}{3}\left(\frac{1}{3}-\frac{1}{4}\right)+...+\)\(\frac{1}{3}\left(\frac{1}{2018}-\frac{1}{2019}\right)\)= \(\frac{1}{3}\left(\frac{1}{2}-\frac{1}{2019}\right)=\frac{2017}{3.2.2019}\)
M+N-P = \(\frac{2017}{6}\left(\frac{1}{2018}+\frac{1}{3.2020}-\frac{1}{2019}\right)\)=\(\frac{2017}{6}.\left(\frac{1}{2018.2019}+\frac{1}{3.2020}\right)\)
= \(\frac{2017\left(1010+1009.673\right)}{3.2018.2019.2020}\)