Cho a>b>0 và a2+3b2=4ab. Tính giá trị phân thức :
A=\(\frac{a+11b}{2a+b}\)
Ai lm xong trc, t tick !!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
0
PT
1
TP
3
TK
19 tháng 11 2021
Ta có a+b=11 ⇒ b=11-a
thay b=11-a vào 2a=b/4 ta có
\(2a=\dfrac{11-a}{4}\)
\(\Leftrightarrow8a=11-a\Leftrightarrow9a=11\Leftrightarrow a=\dfrac{11}{9}\)
với a =\(\dfrac{11}{9}\) thì b=11-\(\dfrac{11}{9}=\dfrac{88}{9}\)
Vậy ...
NN
1
27 tháng 11 2016
Ta có: \(3a^2+b^2=4ab\Rightarrow4a^2-4ab+b^2-a^2=0\Rightarrow\left(2a-b\right)^2-a^2=0\)
\(\Rightarrow\left(2a-b-a\right)\left(2a-b+a\right)=0\Rightarrow\left(a-b\right)\left(3a-b\right)=0\)
Để đẳng thức xảy ra \(\Rightarrow\left[\begin{array}{nghiempt}a-b=0\\3a-b=0\end{array}\right.\)\(\Rightarrow\left[\begin{array}{nghiempt}a=b\\3a=b\end{array}\right.\)
theo đề ra thì b>a>0 => không xảy ra trường hợp a=b.
\(\Rightarrow\frac{a-b}{a+b}=\frac{a-3a}{a+3a}=\frac{-2a}{4a}=-\frac{1}{2}\)
P/s: Không biết cách trình bày có đc không a~
HH
0
CM
3 tháng 1 2018
Chọn D.
Đặt t = 3 x + 1 → t 2 = 3 x + 1 ⇒ d x = 2 3 t d t x = t 2 - 1 2 Đổi cận x = 1 → t = 2 x = 5 → t = 4
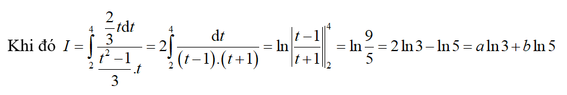
Suy ra a = 2; b = -1 ⇒ a2 + ab + 3b2 = 5.
S
28 tháng 8 2018
Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)
Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)
Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)
Mà a > b > 0 => M = 3
D
30 tháng 8 2018
Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)
Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)
Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)
Mà \(a>b>0\Rightarrow M=3\)
a2 + 3b2 = 4ab
=> a2 + b2 + 2b2 - 2ab - 2ab = 0
=> (a2 - 2ab + b2) - 2b(a - b) = 0
=> (a - b)2 - 2b(a - b) = 0
=> (a - b)(a - b - 2b) = 0
=> (a - b)(a - 3b) = 0
*Xảy ra 2 trường hợp: a - b = 0 => a = b (vô lí vì a > b > 0)
và a - 3b = 0 => a = 3b
Vậy A = ...................Bạn thay a = 3b vào A là xong
Đúng rồi !!