Cho 3 a 2 + 3 b 2 = 10 a b và b > a > 0. Tính giá trị của biểu thức...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

6 tháng 4 2017

Cho 3 a 2 + 3 b 2 = 10 a b và b > a > 0. Tính giá trị của biểu thức P = a - b a + b

#Toán lớp 8

Cao Minh Tâm

6 tháng 4 2017

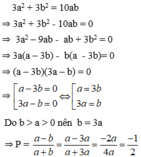
Tìm giá trị của phân thức khi biến thỏa mãn điều kiện cho trước | Toán lớp 8

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Nguyễn Khánh Linh

25 tháng 12 2015 - olm

Bài 1: Cho xyz=2 và x+y+z=0. Tính giá trị của biểu thức: N=(x+y)(y+z)(x+z)

Bài 2: Tính giá trị biểu thức: 3a-2b / a-3b với a/b= 10/3

Bài 5: Tính giá trị của biểu thức: a-8 / b-5 - 4a-b / 3a+3 với a-b=3

#Toán lớp 8

Phạm Anh Tuấn

2 tháng 1 2023 - olm

a) Tìm giá trị nhỏ nhất của biểu thức \(x^2-8x+5\)

b) Cho \(a^3+b^3+c^3=3abc\) và \(a+b+c\) ≠ 0

Tính giá trị của biểu thức N =\(\dfrac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)

#Toán lớp 8

Nguyen xuan truong

12 tháng 11 2017 - olm

Cho a,b > 0 và a+b=a^2+b^2=a^3+b^3

tính giá trị của biểu thức : P = a^2011+b^2015

#Toán lớp 8

Lil Shroud

10 tháng 2 2021

Cho 2 số thực a, b thỏa mãn ab ≠ 0, a ≠ 1, b ≠ 1 và a + b = 1. Tính giá trị của biểu thức

\(P=\dfrac{a}{b^3-1}-\dfrac{b}{a^3-1}+\dfrac{2\left(a-b\right)}{a^2b^2+3}\)

#Toán lớp 8

Lil Shroud

10 tháng 2 2021

Cho 2 số thực a, b thỏa mãn ab ≠ 0, a ≠ 1, b ≠ 1 và a + b = 1. Tính giá trị của biểu thức

\(P=\dfrac{a}{b^3-1}-\dfrac{b}{a^3-1}+\dfrac{2\left(a-b\right)}{a^2b^2+3}\)

#Toán lớp 8

Akai Haruma

Giáo viên

17 tháng 2 2021

Lời giải:

\(P=\frac{a^4-a-b^4+b}{(b^3-1)(a^3-1)}+\frac{2(a-b)}{a^2b^2+3}\)

\(=\frac{(a^4-b^4)-(a-b)}{a^3b^3-(a^3+b^3)+1}+\frac{2(a-b)}{a^2b^2+3}=\frac{(a-b)[(a+b)(a^2+b^2)-1]}{a^3b^3-[(a+b)^3-3ab(a+b)]+1}+\frac{2(a-b)}{a^2b^2+3}\)

\(=\frac{(a-b)[(a^2+b^2)-(a+b)^2]}{a^3b^3-[1-3ab]+1}+\frac{2(a-b)}{a^2b^2+3}=\frac{-2ab(a-b)}{a^3b^3+3ab}+\frac{2(a-b)}{a^2b^2+3}\)

\(=\frac{-2(a-b)}{a^2b^2+3}+\frac{2(a-b)}{a^2b^2+3}=0\)

Đúng(0)

Akai Haruma

Giáo viên

17 tháng 2 2021

Lời giải:

\(P=\frac{a^4-a-b^4+b}{(b^3-1)(a^3-1)}+\frac{2(a-b)}{a^2b^2+3}\)

\(=\frac{(a^4-b^4)-(a-b)}{a^3b^3-(a^3+b^3)+1}+\frac{2(a-b)}{a^2b^2+3}=\frac{(a-b)[(a+b)(a^2+b^2)-1]}{a^3b^3-[(a+b)^3-3ab(a+b)]+1}+\frac{2(a-b)}{a^2b^2+3}\)

\(=\frac{(a-b)[(a^2+b^2)-(a+b)^2]}{a^3b^3-[1-3ab]+1}+\frac{2(a-b)}{a^2b^2+3}=\frac{-2ab(a-b)}{a^3b^3+3ab}+\frac{2(a-b)}{a^2b^2+3}\)

\(=\frac{-2(a-b)}{a^2b^2+3}+\frac{2(a-b)}{a^2b^2+3}=0\)

Đúng(0)

❄Đờ[̲̅i̲̅]❤Là❤Bể❤K[̲̅h̲̅]ổ☠

19 tháng 2 2019 - olm

Cho a>0, b>0, ab= 3, a²+ b²=10. Tính giá trị của biểu thức:

B= 16/( a²- b²)

#Toán lớp 8

Hiếu

19 tháng 2 2019

\(B=\frac{16}{\left(a-b\right)\left(a+b\right)}\)

Ta có : \(a^2+2ab+b^2=10+2ab=16\)

<=>\(\left(a+b\right)^2=16\) Vì a, b đều dương nên ta có : \(a+b=4\)

Mặt khác ta lại có : \(a^2-2ab+b^2=10-2ab=4\)

<=> \(\left(a-b\right)^2=4\)<=> \(\orbr{\begin{cases}a-b=4\\a-b=-4\end{cases}}\)

=> Bạn thay vào B tính nha

Đúng(0)

❄Đờ[̲̅i̲̅]❤Là❤Bể❤K[̲̅h̲̅]ổ☠

19 tháng 2 2019

Tặng cho 3

Đúng(0)

trần công phúc

17 tháng 9 2017 - olm

tính giá trị của biểu thức a) cho a+b=5 ab=6 tính a^3+b^3

b)cho a+b=1 tính giá trị của 2.(a^3+b^3)-3.(a^2+b^2)

#Toán lớp 8

Phương Bùi Mai

2 tháng 12 2018 - olm

Cho a³+b³+c³ =3abc và a+b+c khác 0.Tính giá trị biểu thức N=\(\frac{a^2+b^2+c^2}{\left(a+b+a\right)^2}\)

Cho a+b=1.Tính giá trị của biểu thức sau M= a³+b³+3ab(a²+b²)+6a²b²(a+b)

Giúp mk vs nha!!Thanks mn nhìuu:))))

#Toán lớp 8

Mất nick đau lòng con quốc quốc

2 tháng 12 2018

\(a^3+b^3+c^3=3abc\)

\(\Leftrightarrow\)\(a^3+b^3+c^3-3abc=0\)

\(\Leftrightarrow\)\(\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc=0\)

\(\Leftrightarrow\)\(\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)=0\)

\(\Leftrightarrow\)\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)

\(\Leftrightarrow\)\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2-3ab\right]=0\)

Do \(a+b+c\ne0\) nên \(\left(a+b\right)^2-c\left(a+b\right)+c^2-3ab=0\)

\(\Leftrightarrow\)\(a^2+b^2+c^2-ab-bc-ca=0\)

\(\Leftrightarrow\)\(2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)

\(\Leftrightarrow\)\(\left(a^2-2ab+b^2\right)+\left(b^2-bc+c^2\right)+\left(c^2-ca+a^2\right)=0\)

\(\Leftrightarrow\)\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)

\(\Leftrightarrow\)\(\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Leftrightarrow a=b=c}\)

\(\Rightarrow\)\(N=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}=\frac{3a^2}{\left(3a\right)^2}=\frac{3a^2}{9a^2}=\frac{1}{3}\)

...

Đúng(0)

Phương Bùi Mai

2 tháng 12 2018

Cảm ơn bạn nha

Đúng(0)

Tuyết Ly

19 tháng 3 2022

Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.

a) Tính giá trị của biểu thức A khi x = 2/3.

b) Chứng minh B = x−1/x .

c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.

#Toán lớp 8

Tuyết Ly

19 tháng 3 2022

Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.

a) Tính giá trị của biểu thức A khi x = 2/3.

b) Chứng minh B = x−1/x .

c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.

#Toán lớp 8

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP