
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{\left(-3\right)^{45}\cdot5^3\cdot2^{12}}{5^4\cdot3^{44}\cdot\left(-2\right)^{11}}=\dfrac{\left(-3\right)^{45}\cdot\left(-2\right)^{12}}{5\cdot\left(-3\right)^{44}\cdot\left(-2\right)^{11}}=\dfrac{\left(-3\right)\cdot\left(-2\right)}{5}=\dfrac{6}{5}\)

a) \(\hept{\begin{cases}2x=5y=8z\\x-2y-3z=0,5\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{5}}=\frac{z}{\frac{1}{8}}\\x-2y-3z=0,5\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{\frac{1}{2}}=\frac{2y}{\frac{2}{5}}=\frac{3z}{\frac{3}{8}}\\x-2y-3z=0,5\end{cases}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{\frac{1}{2}}=\frac{2y}{\frac{2}{5}}=\frac{3z}{\frac{3}{8}}=\frac{x-2y-3z}{\frac{1}{2}-\frac{2}{5}-\frac{3}{8}}=\frac{0,5}{-\frac{11}{40}}=\frac{-20}{11}\)
=> x = -10/11 ; y = -4/11 ; z = -5/22
b) \(\hept{\begin{cases}0,2a=0,3b=0,4c\\2a+3b-5c=-1,8\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a}{5}=\frac{b}{\frac{10}{3}}=\frac{c}{\frac{5}{2}}\\2a+3b-5c=-1,8\end{cases}}\Rightarrow\hept{\begin{cases}\frac{2a}{10}=\frac{3b}{10}=\frac{5c}{\frac{25}{2}}\\2a+3b-5c=-1,8\end{cases}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2a}{10}=\frac{3b}{10}=\frac{5c}{\frac{25}{2}}=\frac{2a+3b-5c}{10+10-\frac{25}{2}}=\frac{-1,8}{\frac{15}{2}}=-\frac{6}{25}\)
=> a = -6/5 ; b = -4/5 ; c = -3/5
c) \(\hept{\begin{cases}a=\frac{3}{4}b=\frac{5}{6}c\\2b-a-c=-39\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a}{1}=\frac{b}{\frac{4}{3}}=\frac{c}{\frac{6}{5}}\\2b-a-c=-39\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a}{1}=\frac{2b}{\frac{8}{3}}=\frac{c}{\frac{6}{5}}\\2b-a-c=-39\end{cases}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{1}=\frac{2b}{\frac{8}{3}}=\frac{c}{\frac{6}{5}}=\frac{2b-a-c}{\frac{8}{3}-1-\frac{6}{5}}=\frac{-39}{\frac{7}{15}}=\frac{-585}{7}\)
=> a = -585/7 ; b = -780/7 ; c = -702/7
a) Ta có :\(\hept{\begin{cases}2x=5y\\3y=8z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{5}=\frac{y}{2}\\\frac{y}{8}=\frac{z}{3}\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{20}=\frac{y}{8}\\\frac{y}{8}=\frac{z}{3}\end{cases}}\Rightarrow\frac{x}{20}=\frac{y}{8}=\frac{z}{3}\Rightarrow\frac{x}{20}=\frac{2y}{16}=\frac{3z}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{20}=\frac{y}{8}=\frac{z}{3}=\frac{2y}{16}=\frac{3z}{9}=\frac{x-2y-3z}{20-16-9}=\frac{0,5}{-5}=-0,1\)
=> x = -2 ; y = -0,8 ; z = -0,3
b) Ta có : \(0,2a=0,3b=0,4c\Rightarrow0,2a.\frac{1}{12}=0,3b.\frac{1}{12}=0,4c.\frac{1}{12}\)
=> \(\frac{a}{60}=\frac{b}{40}=\frac{c}{30}\Rightarrow\frac{2a}{120}=\frac{3b}{120}=\frac{5c}{150}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\frac{a}{60}=\frac{b}{40}=\frac{c}{30}=\frac{2a}{120}=\frac{3b}{120}=\frac{5c}{150}=\frac{2a+3b-5c}{120+120-150}=\frac{-1,8}{90}=-0,02\)
=> a = -1,2 ; b = -0,8 ; c = -0,6
c) \(\frac{2}{3}a=\frac{3}{4}b=\frac{5}{6}c\)
=> \(\frac{2}{3}a.\frac{1}{30}=\frac{3}{4}b.\frac{1}{30}=\frac{5}{6}c.\frac{1}{30}\Rightarrow\frac{a}{45}=\frac{b}{40}=\frac{c}{36}\Rightarrow\frac{a}{45}=\frac{2b}{80}=\frac{c}{36}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{45}=\frac{b}{40}=\frac{c}{36}=\frac{2b}{80}=\frac{2b-a-c}{80-45-36}=\frac{-39}{-1}=39\)
=> a = 1755 ; b = 1560 ; c = 1404

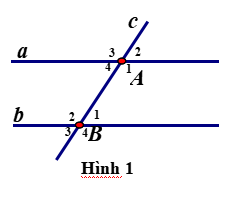
\(a,\text{So le trong: }\widehat{A_1}\text{ và }\widehat{B_2}\\ \text{Đồng vị: }\widehat{A_1}\text{ và }\widehat{B_4}\\ b,a\text{//}b\Rightarrow\widehat{A_1}=\widehat{B_2}=42^0\\ \Rightarrow\widehat{B_1}=180^0-\widehat{B_2}=138^0\left(\text{kề bù}\right)\)
giúp mik tìm thêm so le trong và đồng vị thêm một cặp góc nx ik bạn

\(a=\frac{5}{3}b\); \(c=\frac{5}{6}b\)
\(\Rightarrow3.\frac{5}{6}b-2.\frac{5}{3}b=10\)
\(\Leftrightarrow\frac{-5}{6}b=10\)
\(\Leftrightarrow b=-12\)
b, Tương tự
Bài làm:
a) \(3a=5b=6c\)
\(\Leftrightarrow\frac{a}{10}=\frac{b}{6}=\frac{c}{5}\)
Áp dụng t/c của dãy tỉ số bằng nhau:
\(\frac{a}{10}=\frac{b}{6}=\frac{c}{5}=\frac{3c-2a}{15-20}=\frac{10}{-5}=-2\)
\(\Rightarrow\hept{\begin{cases}a=-20\\b=-12\\c=-10\end{cases}}\)
b) Ta có: \(3a=4b\Leftrightarrow\frac{a}{4}=\frac{b}{3}\Leftrightarrow\frac{a}{20}=\frac{b}{15}\left(1\right)\)
và \(6b=5c\Leftrightarrow\frac{b}{5}=\frac{c}{6}\Leftrightarrow\frac{b}{15}=\frac{c}{18}\left(2\right)\)
Từ (1) và (2) => \(\frac{a}{20}=\frac{b}{15}=\frac{c}{18}\)
Áp dụng t/c của dãy tỉ số bằng nhau:
\(\frac{a}{20}=\frac{b}{15}=\frac{c}{18}=\frac{2c-3b+a}{36-45+20}=\frac{-22}{11}=-2\)
\(\Rightarrow\hept{\begin{cases}a=-40\\b=-30\\c=-36\end{cases}}\)

Ta có:
\(\frac{a}{5}=\frac{b}{-4}=\frac{a-b}{5-\left(-4\right)}=\frac{a-2b}{5-2\left(-4\right)}\)
Mà a - 2b = 26
\(\Rightarrow\frac{a-b}{5-2\left(-4\right)}=\frac{26}{13}=2\)
\(\Rightarrow\frac{a}{5}=2\)
\(a=2.5=10\)
\(\Rightarrow\frac{b}{-4}=2\)
\(b=2.\left(-4\right)=-8\)
Vậy a = 10
b = -8
Có : \(\frac{b}{-4}=\frac{2b}{-8}\)
Do \(\frac{a}{5}=\frac{b}{-4}\Rightarrow\frac{a}{5}=\frac{2b}{-8}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có :
\(\frac{a}{5}=\frac{2b}{-8}=\frac{a-2b}{5-\left(-8\right)}=\frac{26}{13}=2\)
\(\Rightarrow\hept{\begin{cases}a=5\cdot2=10\\2b=-8\cdot2=-16\Rightarrow b=\frac{-16}{2}=-8\end{cases}}\)

1. 4x/6y=(2x+8)/(3y+11) <=> 12xy+44x=12xy+48y
<=> 44x=48y =>x/y=12/11
mình chỉ biết câu 1 thôi :v

Ta có a+b=11 ⇒ b=11-a
thay b=11-a vào 2a=b/4 ta có
\(2a=\dfrac{11-a}{4}\)
\(\Leftrightarrow8a=11-a\Leftrightarrow9a=11\Leftrightarrow a=\dfrac{11}{9}\)
với a =\(\dfrac{11}{9}\) thì b=11-\(\dfrac{11}{9}=\dfrac{88}{9}\)
Vậy ...
Uki