tìm các số a và b biết 900:(a+b)=ab
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
19 tháng 7 2015
ab*(a + b) = 900 => ab chia hết cho 3 - do vậy a + b cũng chia hết cho 3 - vì ngược lại thì cả (ab) và a + b đều không chia hết cho 3 nên tích (ab)*(a + b) không chia hết cho 3. Mặt khác (a + b) không chia hết cho 9 vì lúc đó cả (ab) và a + b đều chia hết cho 9 => (ab)*(a + b) chia hết cho 9², không thể.
9 < 900 / 99 ≤ 900 / (ab) = a + b
=> a + b chỉ có thể là 12 hoặc 15
Với a + b = 12 => (ab) = 900 / 12 = 75 (thỏa với a = 7, b = 5)
Với a + b = 15 => (ab) = 900 / 15 = 60 (loại)
10 tháng 7 2016
Giải
Biến đổi bất đẳng thức đã cho thành phép nhân : ab . ( a + b ) = 900.
Như vậy ab và a + b là cácc ước của 900. Ta có các nhận xét :
a) a + b < 18 ;
b) ab < 100 nên a + b > 9
c) Tích ab ( a + b ) chia hết cho 3 nên tồn tại một thừa số chia hết cho 3.
Do ab và a + b có cùng số dư trong phép chia cho 3 nên cả hai cùng chia hết cho 3.
Từ ba nhận xét đó, ta có a + b bằng 12, hoặc 15, hoặc 18.
Nếu a + b = 12 thì ab = 900 : 12 = 75, thỏa mãn 7 + 5 = 12.
Nếu a + b = 15 thì ab = 900 : 15 = 60, loại
Nếu a + b = 18 thì ab = 900 : 18 = 50, loại
Ta có đáp số : a = 7, b = 5
10 tháng 7 2016
Câu hỏi của Hatsune Miku - Toán lớp 6 - Học toán với OnlineMath
TO
0
GV
0
NT
1
PT
1
PT
1
CM
11 tháng 9 2018
Vì (a,b) = 10 nên a = 10x, b = 10y, với (x,y)=1
Suy ra a.b=10x.10y = 100xy.
Lại có a.b = [a,b].(a,b) = 900.10 = 9000
Suy ra 100xy = 9000 => xy = 90
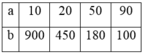
Giả sử x<y và (x,y)=1 ta có các trường hợp sau:
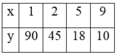
Từ đó suy ra a,b có các trường hợp sau:
